RESEARCH/REVIEW ARTICLE
A model study of the first ventilated regime of the Arctic Ocean during the early Miocene
Bijoy Thompson,1 Martin Jakobsson,1 Johan Nilsson,2 Jonas Nycander2
& Kristofer Döös2
1 Department of Geological Sciences, Stockholm University, Stockholm SE-10691, Sweden
2 Department of Meteorology, Stockholm University, Stockholm SE-10691, Sweden
Abstract
The tectonic opening of Fram Strait during the Neogene was a significant geological event that transferred the Arctic Ocean from a poorly ventilated enclosed basin, with weak exchange with the North Atlantic, to a fully ventilated “ocean stage”. Previous tectonic and physical oceanographic analyses suggest that the early Miocene Fram Strait was likely several times narrower and less than half as deep as the present-day 400 km wide and 2550 m deep strait. Here we use an ocean general circulation model with a passive age tracer included to further address the effect of the Fram Strait opening on the early Miocene Arctic Ocean circulation. The model tracer age exhibits strong spatial gradient between the two major Arctic Ocean deep basins: the Eurasian and Amerasian basins. There is a two-layer stratification and the exchange flow through Fram Strait shows a bi-layer structure with a low salinity outflow from the Arctic confined to a relatively thin upper layer and a saline inflow from the North Atlantic below. Our study suggests that although Fram Strait was significantly narrower and shallower during early Miocene, and the ventilation mechanism quite different in our model, the estimated ventilation rates are comparable to the chemical tracer estimates in the present-day Arctic Ocean. Since we achieved ventilation of the Arctic Ocean with a prescribed Fram Strait width of 100 km and sill depth of 1000 m, ventilation may have preceded the timing of a full ocean depth connection between the Arctic Ocean and North Atlantic established through seafloor spreading and the development of the Lena Trough.
Keywords
Ocean modelling; Miocene Arctic Ocean; palaeoceanography; ocean ventilation; age tracer.
Correspondence
Bijoy Thompson, Department of Geological Sciences, Stockholm University, Stockholm SE-10691, Sweden. E-mail: bijoymet@gmail.com
(Published: 30 July 2012)
Polar Research 2012. © 2012 B. Thompson et al. This is an open-access article distributed under the terms of the Creative Commons Attribution-Noncommercial 3.0 Unported License (http://creativecommons.org/licenses/by-nc/3.0/), permitting all non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Citation: Polar Research 2012, 31, 10859, http://dx.doi.org/10.3402/polar.v31i0.10859
The components influencing the global climate system over timescales of 104–106 years include the variations in the Earth's orbital geometry, the continental geography and topography, the configuration of oceanic basins and gateways, and the concentrations of the atmospheric greenhouse gases. The complex dynamics of these components have driven Earth's climate through the Cenozoic transition from what commonly is referred to as a Greenhouse to an Icehouse World (Zachos et al. 2001). Of the tectonic boundary conditions, the variations in ocean gateways have in particular imposed significant changes to the global ocean circulation and physical properties of sea water in different basins (Zachos et al. 2001; von der Heydt & Dijkstra 2006). One of the most widely known examples in palaeoceanography is the Mediterranean Sea's isolation from Atlantic Ocean 5.6 million years ago (Mya) which resulted in a following period of severe evaporation referred to as the Messinian salinity crisis (Krijgsman et al. 1999). The spectacular flooding 5.33 Mya, called the Zanclean flood event and caused by the tectonic subsidence of Gibraltar Strait, changed the palaeoceanographic conditions in the Mediterranean Sea (Garcia-Castellanos et al. 2009). Much like the late Miocene Mediterranean Sea, the Arctic Ocean was landlocked during most of the Cenozoic, implying that its palaeoceanographic evolution was for long periods disconnected from the rest of the World Oceans (O'Regan et al. 2011). However, a comprehensive investigation of the Arctic Ocean Cenozoic palaeo-environmental history has been restrained by the scarcity of continuous geological records. It was only in 2004, when the Integrated Ocean Drilling Program (IODP) Expedition 302, the Arctic Coring Expedition (ACEX), retrieved the first long drill core from the central Arctic Ocean, that proposed tectonic models with palaeoceanographic implications could be compared with geological ground truth (Backman et al. 2006). The 428 m long sediment record retrieved from the Lomonosov Ridge unveiled a range of novel results (e.g., Brinkhuis et al. 2006; Moran et al. 2006; Pagani et al. 2006; Sluijs et al. 2006; Jakobsson et al. 2007; Haley et al. 2008; Backman & Moran 2009). One of these results suggests that the Arctic Ocean transformed from a poorly oxygenated “lake stage” to a fully oxygenated “ocean stage” during late early Miocene (17.5 Mya; Jakobsson et al. 2007). The authors link this ventilation change to the tectonic opening of Fram Strait; the major ocean gateway between the Arctic and Atlantic oceans located between Greenland and Svalbard (Fig. 1). Furthermore, from a two-layer analytical model the transition to a fully oxygenated Arctic Ocean regime is estimated to have happened when Fram Strait first reached a width of about 40–50 km. They also estimated that with an inflow of 1.5 Sv (1 Sv = 106 m3/s) from the Atlantic Ocean, the ventilation time may be less than 250 years.
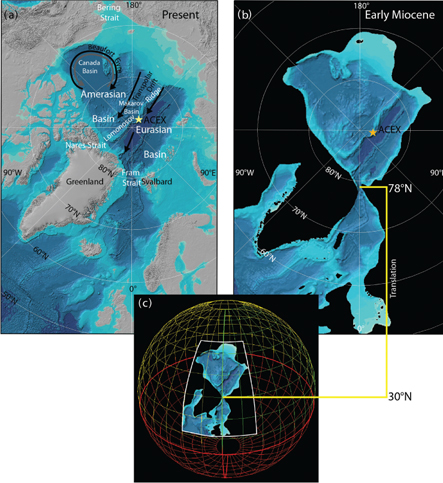
Fig. 1
(a) The present Arctic Ocean portrayed by the International Bathymetric Chart of the Arctic Ocean (IBCAO; Jakobsson et al. 2008). The two major present-day surface circulation features, the Transpolar Drift and Beaufort Gyre, are shown. The Beaufort Gyre has generally two predominant regimes; one anticyclonic (black: September–May) and one cyclonic (grey: June–August) (Proshutinsky et al. 2002). (b) The reconstructed palaeo-bathymetry representing the early Miocene Arctic Ocean. The IBCAO grid shown in (a) was used as base data for this reconstruction (see text for further information). (c) The palaeo-bathymetric grid was translated so that the geographic position 78°N 0°E, located in the centre of Fram Strait, was moved to 30°N 0°E in order to avoid problems associated with having the North Pole included in the simulations.
Here we use an ocean general circulation model (OGCM) specifically configured for the late early Miocene Arctic Ocean basin to further address the Arctic Ocean's initial stage as a ventilated ocean with a connection to the North Atlantic Ocean through Fram Strait. Our diagnostics of the OGCM results are aimed at examining the spatial variation of the ventilation in the early Miocene Arctic Ocean. There are some specific questions that we want to study qualitatively. First, how representative are palaeoceanographic proxies of the oxygen content at the ACEX coring sites for the ventilation state of the early Miocene Arctic Ocean? More specifically, can strong spatial gradients in ventilation be expected near the ACEX sites, making the relation between local ventilation and the Fram Strait flow sensitive to the palaeo-depths and locations of the sites on the Lomonosov Ridge? In addition, we follow up a few open question of principle nature that arose in a related study by Thompson et al. (2010), which was based on highly idealized model simulations of the early Miocene Arctic Ocean physiographic setting. In particular, Thompson et al. (2010) made simulations for a basin with a volume approximately 10 times smaller than that of the Arctic Ocean in the relevant geological period. The present numerical experiment allows testing the volume dependence of the ventilation proposed by Thompson et al. (2010).
Methods and boundary conditions
Ocean ventilation and diagnostics
Turnover time and age are concepts often used to describe the ventilation timescale in an ocean basin. The turnover time (τ0) is an integral quantity that gives a bulk estimate of the ventilation time in a basin. It is defined as the time taken by a substance to fill a basin, or the time taken to renew the substance in a basin. The age of a water parcel is the time elapsed since it left the region where age is set to zero. Often this region is the surface, but here it will be taken to be the North Atlantic Ocean south of Fram Strait.
The use of natural and anthropogenic tracer inventories such as tritium (3H), radiocarbon (14C) or chlorofluorocarbons (CFCs) provides independent means for studying the ventilation time scale of water masses (Timmermans et al. 2005; Tanuha et al. 2009). Studies using these tracer inventories estimated the present mean age of deep waters in the Eurasian Basin to be about 200–300 years (Schlosser et al. 1997; Timmermans et al. 2005; Tanuha et al. 2009). The deep waters in the Canada Basin are older, with a mean age estimate of 450 years (Schlosser et al. 1997). From using CFC inventories, the present-day upper limit of ventilation timescale in the deep Arctic Ocean waters is approximated to 500–600 years (Tanuha et al. 2009). However, the ventilation rate can vary substantially within a basin. Such spatial variation can be studied by using OGCMs instead of analysing discrete samples of tracers. One approach for this is the Lagrangian dispersion, where Lagrangian trajectories are computed from the velocity fields of an ocean circulation model (Johnson et al. 2004; Döös et al. 2008). Another approach involves integrating the numerical ocean circulation model with passive tracers (Cox 1989; England 1995; Deleersnijder et al. 2001; Deleersnijder et al. 2002). The prognostic passive age tracer is integrated using the advection–diffusion equation, similar to that used for the active tracers (temperature and salt).
Thompson et al. (2010) carried out a study of the ventilation timescale using the Geophysical Fluid Dynamics Laboratory Modular Ocean Model 4 (MOM4p1; Griffies 2007) and an idealized ocean basin. In this present work we use MOM4p1, and build our diagnostics of the ventilation time and its spatial distribution on the experience gained from the Thompson et al. (2010) study. Their model bathymetry was an idealized representation of the North Atlantic–Fram Strait–Arctic Ocean system, and consisted of two semi-enclosed basins connected with a strait over a sill. A series of model experiments were performed for different strait widths (96 km or 325 km), sill depths (1000 m or 250 m) and freshwater fluxes (0.16 Sv or 0.2 Sv), with and without wind stress. In the wind forced experiments a cyclonic wind stress was applied as: the zonal wind stress, 
Here, A=0.1 N/m2 is the maximum value of wind stress, L is the total length of the model domain, and y is the distance from the southern boundary. Their experiment with a reduced sill depth (sill depth was reduced by a factor of 4) showed that the sill depth has an insignificant effect on the tracer age distribution in the absence of wind forcing. The maximum tracer age has increased by only about 8% in their study. Consistent with the theoretical models of strait flows (Pratt & Spall 2008), the study suggested that the exchange flow is essentially independent of the sill depth as long as the upper layer is shallower than the sill depth. In general, the sensitivity experiments illustrated that as the strait width decreases, the tracer age increases. The reduction in the width of the strait by a factor of about 3.5 leads in the present simulations to an increase of the tracer age by about 15–20%. The study revealed that the mean age (τmean) in the basin was underestimated by the turnover time in the experiments with wider strait widths, while for narrow straits the turnover time overestimated the mean age. It should be noted that the strait widths (325 and 96 km) used by Thompson et al. (2010) are much larger than the Rossby radius (ca. 10 km) in their simulations. Jakobsson et al. (2007) estimated the onset of fully ventilated conditions in the early Miocene Arctic Ocean based on the bulk quantity turnover time for a strait narrower than the one used by Thompson et al. (2010). Based on how the ratio between mean age and turnover time depended on strait width, it was concluded that the timescale estimate (ca. 250 years) by Jakobsson et al. (2007) provides an upper limit of mean ventilation time in the early Miocene Arctic Ocean.
One objective of the present study is to understand the relationship between the turnover time and mean tracer age in the early Miocene Arctic Ocean. A detailed investigation of the spatial variation of ventilation time scale in different sub-basins within the Arctic Ocean has been performed. We integrated MOM4p1 together with a prognostic passive age tracer and forced by freshwater flux.
Early miocene palaeo-bathymetry
The palaeo-bathymetry of the early Miocene Arctic Ocean was reconstructed by “morphing” the International Bathymetric Chart of the Arctic Ocean (IBCAO) gridded database (Jakobsson et al. 2008), using information from tectonic modelling and geological records. For details about the morphing techniques and geological source data see Jakobsson et al. (2007). The reconstructed palaeo-bathymetric grid is based on Cartesian coordinates with the same projection and datum as IBCAO, i.e., a polar stereographic projection with the centre of origin at the North Pole, true scale at 75°N, and the World Geodetic System of 1984 (WGS 84) horizontal datum (Fig. 1). In order to avoid the numerical instability due to the singularity at the North Pole the grid was translated so that the geographic position 78°N, 0°E in Fram Strait was moved to 30°N, 0°E. This translation was carried out on the polar stereographic projection plane. Subsequent to the translation, the Cartesian grid was re-projected to latitude-longitude coordinates and sub-sampled to a regular horizontal resolution of 0.22°×0.22° (Fig. 1c). In the final bathymetric grid used in the model, this resolution was kept in a 5°×5° box centred on Fram Strait (Fig. 2). Beyond this box the zonal and meridional resolution were stretched to 0.6° at a distance of 10° from Fram Strait centre and to 1° at the lateral boundaries of the full grid.
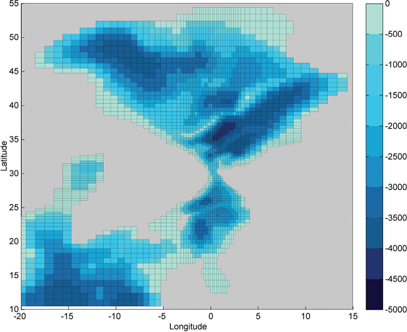
Fig. 2
Stretched grid representing the early Miocene bathymetry in the MOM4p1 simulations presented in this paper. The latitude and longitude correspond to the remapped grid.
There are numerous inherent uncertainties in the reconstructed palaeo-bathymetry due to lack of constraining geological data (Jakobsson et al. 2007). However, the resolution of the stretched bathymetric grid used in our simulations implies that only major bathymetric features will likely have an impact on the circulation. These features will be briefly discussed.
The first of these is the Lomonosov Ridge, which exerts a significant oceanographic influence since it separates the Arctic Ocean into two deep major basins: the Eurasian and Amerasian basins (Fig. 1a). (The Amerasian Basin is further subdivided into the Canada and Makarov basins.) The recorded minimum depth of ocean above the central Lomonosov Ridge is about 607 m in the present-day Arctic Ocean (Jakobsson et al. 2008). The shallowest location of the ridge crest is made approximately 200 m shallower in the early Miocene reconstruction compared to present. This is a conservative depth estimate as the ridge may even have been shallower at that time considering that its subsidence likely was stalled since the time of rifting due to compressional tectonic forces in the Eurasian Basin (O'Regan et al. 2008). Furthermore, the ACEX drill sites on the Lomonosov Ridge crest are located >130 km closer to the Barents and Kara Sea shelf in the palaeo-bathymetry, since the seafloor spreading had not yet fully developed the Eurasian Basin. The earliest recorded migration of the marine bivalve mollusc Astarte from the Arctic Ocean into the North Pacific has been suggested to constrain the Cenozoic opening, or flooding, of the Bering Strait to about 5.4–5.5 Mya (Gladenkov et al. 2002). However, recent investigations of the Tjörnes section on Iceland showed that invasion of Pacific molluscs, likely linked to the first Cenozoic flooding of the Bering Strait, occurred first at about 4.5 Mya (Verhoeven et al. 2011).
Prior to this, the strait had been closed since Cretaceous times, implying that there was no Arctic Ocean connection to the North Pacific Ocean throughout most of the Cenozoic. From this information and drilled wells on the Alaskan continental margin (see Jakobsson et al. 2007), the Bering Strait is kept completely closed in the early Miocene palaeo-bathymetry. The palaeogeographic maps by Torsvik et al. (2002) indicate no marine passage through the Nares Strait for time slices representing Palaeocene, late Oligocene, early middle Miocene and middle Pliocene times and, therefore, this strait is closed in our simulations. The Barents Shelf has been subjected to several periods of uplift since the late Oligocene 28.4 Mya (Torsvik et al. 2002). In the palaeo-geographic reconstructions by Torsvik et al. (2002) the late Oligocene to middle Miocene interval is portrayed as the so-called Barents Platform. As there are no direct evidences to signify that an ocean passage existed in the Barents Shelf during early Miocene this passage is also closed in our model palaeo-bathymetry, conforming to the reconstruction of Jakobsson et al. (2007).
Finally, one of the main motivations for our simulation experiment is to address the oceanographic consequences, with a particular focus on ventilation, of a much narrower and shallower Fram Strait than at present. The narrowest part of the strait is represented by four 0.22°×0.22° grid cells across, implying a width of slightly less than 100 km compared to the present width of approximately 400 km. The present sill depth at Fram Strait is 2550 m (Klenke & Schenke 2002). Since our experiment address the ventilation some time after the initial opening of Fram Strait in the late early Miocene, we assigned a significantly shallower sill depth of 1000 m. However, we acknowledge that there is no palaeo-information available to constrain this depth.
Ocean temperature, salinity and freshwater forcing
In our model simulation, the temperature is not included and the density is taken to be a function of salinity only. This decision was made primarily to reduce the complexity of the simulation, but was also motivated by indications that the equator-to-pole oceanic temperature difference during the early Miocene likely was smaller than at present (e.g., Zachos et al. 2001). Hence, we assume that during the Miocene the water exchange between the North Atlantic and the Arctic Ocean was mainly controlled by salinity-related density differences. Even in the present-day Arctic Ocean, the density variations tend to be dominated by differences in salinity. However, the three-layer structure of the present-day Arctic stratification, with an intermediate warmer Atlantic layer, depends crucially on temperature variations (Rudels 1995; Rudels et al. 2005). Since these temperature variations are not included in the model, such a three-layer structure is absent in our simulations. In general, the stratification as well as the dynamics becomes more complex when the density depends on both salinity and temperature (e.g., Rudels 1995; Nilsson & Walin 2010). However, the present-day cold bottom layer in the Arctic Ocean, encountered below the intermediate Atlantic layer, is intimately related to the formation of sea ice on the shelves (e.g., Rudels 1995). Given that the early Miocene was warmer than today, it is conceivable that the cold bottom layer was replaced by warmer Atlantic water. In fact, the early Miocene climate model simulation of Herold et al. (2012) yields a salinity-dominated two-layer like stratification in the Arctic, with a colder low-salinity surface layer above a slightly warmer saline Atlantic layer that essentially extends to the bottom. We will here briefly discuss some of the available reconstructions of the oceanographic and climatic conditions in the Arctic during Miocene.
From oxygen isotope analysis of fish bones in the ACEX cores, Waddell & Moore (2008) reconstructed the salinity and the temperature from early Eocene to early Miocene (ca. 55 to ca. 18 Mya). Their reconstructed salinities and temperatures are shown in Fig. 3 (based on Table 3; Waddell & Moore 2008). Fish bone carbonate extracted from apatite is considered to represent burial conditions at the seafloor rather than the water conditions in which the fish lived, implying that the temperatures and salinities by Waddell & Moore (2008) likely represent the palaeo-depth of the Lomonosov Ridge crest. Their analysed early Miocene sample provided a temperature of about 6°C and salinity of about 35 psu. This suggests that the Miocene Arctic Ocean was much warmer than at present. Modern observations show that the salinity on the Lomonosov Ridge crest at 1000 m water depth is also close to 35 psu but the temperature is about −0.4°C (Björk et al. 2007). However, the temperature reconstruction of Waddell & Moore (2008) represents a single depth at the crest of the Lomonsov Ridge and provides no direct information on the vertical temperature stratification. It cannot be ruled out that there were colder water masses, formed on the shelves during winter, in the deep parts of the Miocene Arctic Ocean. Therefore, alternatively, the warm water temperatures in the reconstruction of Waddell & Moore (2008) may indicate that the depth of the Lomonosov Ridge was shallower in the Miocene, implying that the ACEX coring site was influenced by warmer near-surface water masses. In fact, this interpretation is in line with the stalled-subsidence scenario proposed by O'Regan et al. (2008). In any case, the results by Waddell & Moore (2008) clearly support the notion that the Arctic Ocean has gone through a transition from an Eocene closed basin, characterized by low salinities and very warm temperatures, considering its high-latitude location, to a colder ocean with higher salinities.
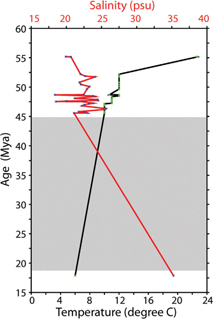
Fig. 3
The temperature and salinity reconstructions from the analysis of fish bones in ACEX 302 M0002A and M0004A. Data are obtained from Waddel & Moore (2008, Table 3). The y axis represents age in millions of years before present (Mya). The black and red line represents the temperature and salinity respectively. The lower x axis is for temperature (°C) and upper x axis is for salinity (psu). The mean salinity value from the computation of Waddel & Moore (2008) is plotted here. The shaded portion indicates the 28 million year long hiatus separating the early Eocene and early Miocene.
There exist no direct proxies for the freshwater input to the Arctic Ocean during the Miocene. However, given that the global mean climate was warmer than at present (Zachos et al. 2001), it is likely that the hydrological cycle was somewhat stronger (Held & Soden 2006). Indications of extensive temperate vegetation over the Arctic continental regions in the Miocene suggest, relative to today, a mild and wet climate (White & Ager 1994). Plant fossils form Devon Island in northern Canada suggest humid, cool to temperate, climate conditions in the oldest part of the Miocene with mean annual terrestrial temperatures between about 8° and 12°C (Hickey et al. 1988). During early to middle Miocene, the occurrence of extreme continental winter temperatures may have been restrained by a warm and ice-free Arctic Ocean (McNeil 1989). In fact, the first Arctic Ocean perennial sea-ice cover was presumably established later, at about 14–13 Mya. This dating is based on the fact that the source areas for ice-rafted sediments analysed in the ACEX record were geographically too far away to have been carried by seasonal sea ice (Darby 2008; Krylov et al. 2008). Therefore, several climate proxies suggest that the early and middle Miocene Arctic climate was much warmer and likely wetter than at present. However, even if the early Miocene Arctic may have been wetter than at present, we decided to follow a conservative approach, and forced our simulations with a freshwater influx similar to today, i.e., 0.2 Sv.
Ocean model and configurations
MOM4p1 is a three-dimensional z-coordinate numerical representation of the hydrostatic primitive equations, employing the Boussinesq approximation and an explicit free surface. The model uses generalized orthogonal coordinates. The salinity advection is handled through the second order moment scheme of Pranther (1986) with flux limiters (Merryfield & Holloway 2003). The age tracer is advected with a multi-dimensional piecewise parabolic scheme based on Colella & Woodward (1984). The horizontal friction scheme is based on the shear-dependent Smagorinsky Laplacian viscosity according to Griffies and Hallberg (2000). The model tracer fields and the baroclinic velocity are time-stepped with 2400 seconds. The barotropic fields have a time step of 20 seconds. The vertical mixing in the model is handled by the K Profile Parameterization Scheme (Large et al. 1994) having local and non-local mixing with a background diffusion of 0.32×10−4 m2/s. The Gent-McWilliams (1990) scheme for parameterization of the sub-grid scale processes is turned off in our model experiments. In the model, density is given as a linear function of the salinity alone:
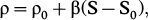
where ρ0
=1035 kg/m3 is the background density, β=0.72 kg/m3/psu is the salinity contraction coefficient, S is the in situ salinity and S0=35 psu is the reference salinity.
As previously described, the model domain has been remapped from the North Pole region to the tropics. The Coriolis parameter was set to the value for 75°N in order to represent the Fram Strait area properly. (This was done for simplicity, but we don't expect the β-effect to be essential, since the Coriolis parameter varies by only a few percent across the basin.) There are 40 vertical levels, which are non-uniformly stretched in depth. In the upper 500 m, the grid distance stretches from 10 m at the surface to 48 m at 500 m with 17 levels. Below this depth the grid box thickness gradually increases to 100 m at 1100 m depth and 325 m in the deepest part of the ocean, with a maximum depth of 4500 m. The model has been initiated with a constant salinity 35 psu. The constant fresh water forcing of 0.2 Sv is applied along the boundaries in the Arctic Ocean, while care has been given to avoid the direct influence of freshwater in Fram Strait by supplying it away from the strait region. To reduce the salinity errors arising due to insufficient coastal mixing, the freshwater is inserted over the upper 40 m in the model. A sponge layer with a width of 8 degrees is applied at the southern boundary of the model, where salinity is relaxed to 35 psu from surface to bottom of the ocean. The relaxation time varies from 10 days at the southern boundary to 100 days at the northern part of the sponge layer.
The model has been integrated with a prognostic passive age tracer. The tracer age (τ) is defined to be zero everywhere at the beginning of model integration, i.e., τ(i,j,k,t)=0. In the Atlantic Ocean (south of Fram Strait) the tracer age is restored to zero at every model time step and it is freely allowed to evolve with model time in the Arctic Ocean. Here, we assumed that the Atlantic Ocean is in a fully ventilated stage. Hence, the water in the Atlantic is assigned with zero tracer age over the entire volume, i.e., τat(i,j,k,t)=0. It should be noted that, in contrast to earlier studies (e.g., England 1995), the age of surface water in the Arctic Ocean is not restored to zero in our experiments. The indefinite growth of tracer age in the Arctic Ocean is limited only by the inflow of zero age water from the North Atlantic Ocean. The model has been integrated for 5000 years to obtain a quasi-equilibrium state. The tracer age presented in this paper correspond to the time average of last 100 years of model integration.
Age distributions.
The distribution of tracer age within the Arctic Ocean and in the water flowing out through Fram Strait is computed based on the frequency functions introduced by Bolin & Rodhe (1973) and further used by Thompson et al. (2010). The frequency function for the age distribution χ is defined as:
where V0 is the total volume of water in the Arctic Ocean, and V(τ) is the volume of water that has spent a time less or equal to τ in the Arctic Ocean.
From the definition of χ, the mean age of the water in the Arctic Ocean (τmean) is given by
The frequency function for the transit time, φ is defined as:
where F0 is the total volume flowing out of the Arctic Ocean and F(τ) is known as the transit time function. It is defined as the volume of water leaving the Arctic Ocean per unit time, having spent a time less than or equal to τ in the Arctic Ocean.
Turnover time.
This parameter is based on the mass balance budget by calculating the total volume of water in the Arctic Ocean and the rate of inflow or outflow. The turnover time (τ0) is defined as the ratio of total volume of water in the Arctic Ocean, V0, to the total outflow through Fram Strait, F0:
Results
Model circulation and salinity
In the present model configuration the Arctic Ocean receives a continuous input of freshwater flux, which provides the necessary buoyancy to generate the ocean currents. The relaxation of salinity to 35 psu in the southern parts of North Atlantic continuously provides high salinity water and thereby balances the freshening of the ocean due to the influx of freshwater into the Arctic Ocean. Since the model is integrated with idealized forcing conditions, the simulation should be considered as a qualitative illustration of a likely Arctic Ocean circulation scenario during the early Miocene. The time mean fields of model salinity and circulation are shown for 5, 500 and 1000 m depths in Fig. 4. The sloping lateral boundaries of the basin give rise to a cyclonic barotropic boundary current (e.g., Nilsson et al. 2005; Spall 2005). This boundary current encircles more than two-thirds of the Arctic Ocean coastline. The freshwater accumulated along the margin of what is today the Canadian Arctic Archipelago and northern Greenland is a major reservoir of the low salinity water transport to the North Atlantic Ocean. The greatest modelled near surface current speeds in the central Arctic Ocean, approximately 0.1 m/s, are found in this area (Fig. 4a).
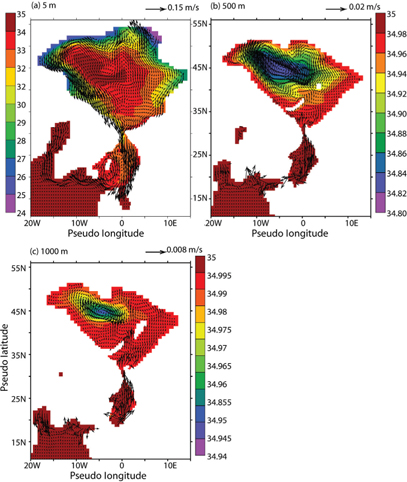
Fig. 4
Salinity (in psu) and circulation (in m/s) (a) at 5 m, (b) at 500 m and (c) at 1000 m from the Early Miocene Arctic Ocean model. The latitude and longitude correspond to the remapped model grid. The shading scale and vector lengths are separately shown for each figure.
An interesting feature in the near surface model circulation is the presence of a cyclonic circulation in the Canada Basin (Fig. 4a). The location of this gyre coincides rather closely with the Beaufort Gyre in the present-day Arctic Ocean (Fig. 1a). Significant variability is observed in the Beaufort Gyre from seasonal to decadal time scales (Steele et al. 2001; Proshutinsky et al. 2002 and references therein). Proshutinsky et al. (2002) described the variability in the Beaufort Gyre circulation in terms of anticyclonic and cyclonic circulation regimes. During boreal winter (September–May), the wind-driven and geostrophic currents coincide to form a strong anticyclonic circulation. It is characterized by a salinity minimum from the surface to 400 m depth and reduced outflow to the North Atlantic Ocean through Fram Strait. In boreal summer (June–August), the winds become weaker, leading to the establishment of a cyclonic circulation regime. The Ekman divergence and upwelling induced by the cyclonic circulation bring saline subsurface water to the upper ocean. This cyclonic circulation increases the transport of freshwater into the North Atlantic. In our simulation (see Fig. 4a), the circulation and salinity field in the Amerasian Basin and the transport path to the North Atlantic Ocean resemble the cyclonic circulation regime described by Proshutinsky et al. (2002).
The simulated exchange circulation in Fram Strait is characterized by an outflow of low-salinity Arctic water in the upper ocean and an inflow of high-salinity Atlantic water below (Fig. 5). The outflow has a thickness of about 200 m, which is shallower than the sill depth of 1000 m. In the strait the isopycnal (i.e., isohaline) surfaces rise toward east, indicating the influence of the rotation on the flow. In fact, the transition from hydraulically to rotationally controlled exchange flows is expected to occur when the strait width becomes comparable to or slightly larger than the internal Rossby radius (e.g., Pratt & Spall 2008). The internal Rossby radius is ca. 8 km in the present simulation, whereas the palaeo Fram Strait width is slightly less than 100 km. According to theory, a rotationally controlled flow is expected with the surface outflow occurring in a wedge attached to the coast, with a width of a few Rossby radii (e.g., Pratt & Spall 2008). However, the simulated outflow is broadly distributed in the strait, with the highest velocities encountered in the central strait. Several factors may contribute to give a broader flow in the simulation than expected from the ideal fluid theory of rotational control. To begin with, there are only four grid points in the strait, which is clearly insufficient for resolving features with scales comparable to the Rossby radius. Further, baroclinic instability and model diffusivity act to broaden any baroclinic current. The present strait flow is, in fact, similar to the one obtained in the “narrow-strait” simulation by Thompson et al. (2010), who also discussed the processes that can make the outflow wider than the internal Rossby radius.
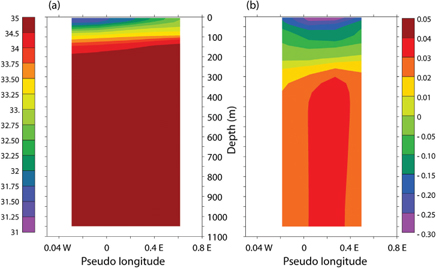
Fig. 5
The longitude-depth sections of (a) salinity (psu) and (b) meridional velocity (m/s) at the middle of Fram Strait. The longitudes correspond to the remapped model grid. Note that there are only four grid points in the strait, which presumably contributes to make the outflow broad.
The simulated stratification in the Arctic Basin has an approximate two-layer structure, with a shallow low-salinity upper layer situated above a deep weakly stratified lower layer (Fig. 6). The lower layer consists of saline water that is advected northward through Fram Strait and gradually mixed with the low-salinity upper-ocean water. A test simulation with the same forcing but a present-day bathymetry, where Fram Strait is significantly wider, yielded a qualitative similar stratification (Fig. 6). In the experiments with idealized bathymetry of Thompson et al. (2010) two-layer structure also emerged for a range of different strait widths and sill depths, and in the absence as well as in the presence of wind forcing. Thus, the simulated two-layer structure of the Arctic arises primarily from the net freshwater input and the exclusion of temperature variations, which precludes the possibility to form a cold but less saline bottom layer.
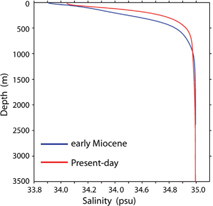
Fig. 6
Vertical distribution of salinity in the central Canada Basin simulated by the models with early Miocene (blue line) and present-day (red line) bathymetries. Below mixed layer the profiles almost overlap each other. The locations of profiles in the remapped grid are 10°W and 47°N.
The present-day three-layer structure of the Arctic Ocean depends critically on the formation of sea ice on the shelves, which creates the cold bottom layer encountered below the intermediate Atlantic layer (e.g., Rudels 1995). During the warmer early Miocene, when the sea-ice formation presumably was weaker, it is likely that the cold bottom layer was absent and that relatively warm Atlantic water layer extended from the bottom up to the low-salinity surface layer. This notion is supported by the early Miocene climate model simulation of Herold et al. (2012), where the Arctic Ocean has an approximate two-layer structure: an upper low salinity layer about 300 m deep with a temperature of about 1°C; and a lower layer Atlantic with a temperature of about 5°C. In the present simulation, this temperature difference would act to diminish the vertical density difference with about 10%. As discussed by Nilsson & Walin (2010) and Thompson et al. (2010), the flow response to such a density change will depend on the features of the vertical mixing. In the present simulation, which uses a fixed vertical diffusivity, a 10% reduction of the vertical density difference is expected to yield a modest (less than 10%) reduction of the flow strength. Fig. 7 shows the meridional overturning stream function computed as functions of latitude and depth as well as latitude and salinity. The stream functions are dominated by an anticlockwise circulation cell, representing the outflow of low salinity water from the Arctic Ocean and inflow of high-salinity water. Also, a weak recirculation cell is seen within the North Atlantic Ocean.
Fig. 7
Meridional overturning stream function (in Sv) computed from the model velocity field as function of (a) latitude and depth and (b) latitude and salinity. The latitudes correspond to the remapped model grid.
The model velocity fields are used to compute the turnover time in the early Miocene Arctic Ocean. In our simulation with freshwater forcing of 0.2 Sv the turnover time is estimated to be 480 years.
Tracer age
The early Miocene Arctic Ocean shows strong spatial variability in tracer age both in the vertical and horizontal directions. The vertical variation of horizontal mean and horizontal maximum ages are shown in Fig. 8. The horizontal mean shows relatively old ages in the upper 250 m, a feature reflecting the outflow of old age water from the Arctic Ocean in the model upper ocean. In the subsurface, below 500 m, the mean age has a constant value of ca. 175 years. However, the maximum age increases with depth and oldest water (about 475 years) is observed at ca. 1700 m. Below this depth, the maximum age shows a gradual reduction. This happens mainly due to the supply of dense inflowing water with low tracer age to the regions below the sill.
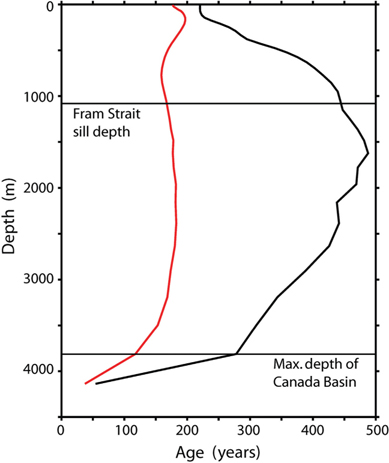
Fig. 8
Vertical variation of the tracer age in Early Miocene Arctic Ocean model, horizontal maximum age (black line) and horizontal average age (red line).
The vertical variation of maximum age is therefore characterized by low values at the surface and bottom regions. The depth of the Canada Basin in our early Miocene palaeo-bathymetry reaches a maximum of about 3800 m (Fig. 2). However, the Eurasian Basin is deeper, which causes the maximum tracer age shown in Fig. 8 to decrease to ca. 50 years below 3800 m as the curve here represents the younger bottom waters in the Eurasian Basin. A reduction in the mean tracer age is for the same reason seen below 3800 m.
The topographic features like ridges, sloping bottom boundaries and closed depth contours are important constraints in determining the flow patterns, thereby regulating the advective tracer transports (e.g., Nøst & Isachsen 2003; Nilsson et al. 2005). In Fig. 8, strong horizontal variations in the tracer age are clearly evident in the age distributions at different depth levels. To certain extent, the bottom topography is imprinted on the horizontal distribution of the tracer age and the salinity in the overlying water column, as shown in Figs. 4 and 9; this tendency is most evident at around 500 m. This reflects the presence of barotropic along isobath currents that arise from bottom density variations (Nilsson et al. 2005). Due to these slope currents, the water near the coasts in the upper ocean is fairly well ventilated and the tracer age is consequently low near the boundaries. The oldest surface water is encountered in the middle part of Canada Basin with an age of about 220 years. This age maximum develops due to the upwelling currents associated with the cyclonic circulation pattern, which brings older water from the subsurface.
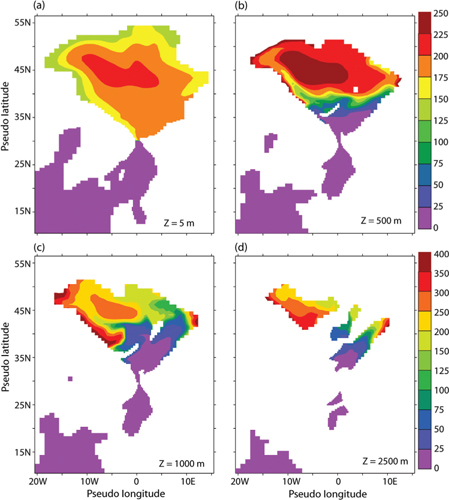
Fig. 9
Modelled tracer age (in years) at different vertical levels at (a) 5 m, (b) 500 m, (c) 1000 m and (d) 2500 m depth. The latitude and longitude correspond to the remapped model grid.
The large gradient in the subsurface tracer age between the Eurasian and Amerasian Basins shows that the Lomonosov Ridge acts as an effective barrier, inhibiting deep water exchange between these two basins. The younger age in the Eurasian Basin is attributed to its relatively efficient water mass exchange with the North Atlantic Ocean. The relatively shallow sill depth in our early Miocene representation of the Lomonosov Ridge restrains the intermediate and deep water inflow to the Amerasia Basin. However, limited water mass exchange is possible through a bathymetric passage in the ridge near the North Pole (Fig. 9b–c). A passage exists here also at present-day and is important for the water mass exchange across the Lomonosov Ridge (Björk et al. 2007), although there is no information available indicating whether this passage was bathymetrically more or less pronounced during the early Miocene compared to the present.
The calculated mean tracer age for our early Miocene Arctic Ocean is about 180 years. However, the mean age exhibits strong variations between the sub-basins. For instance, in the Canada Basin the mean tracer age is higher than 240 years, while the mean ages are as low as 100 and 140 years in the Eurasia and Makarov basins, respectively. The oldest water in the Arctic Ocean is found at middle depths in the Canada Basin, which has an age of about 475 years. In contrast, the maximum tracer age in the Eurasia Basin is less than 200 years.
The latitude-depth sections of zonal maximum, zonal minimum and zonal average tracer age are drawn in the Fig. 10. The intrusion of young water from the North Atlantic at intermediate depths above the sill and outflow of relatively old water in the upper ocean is evident in Fig. 10. The inflowing dense and young water flows down the slopes north of Fram Strait and efficiently ventilates the bottom water in the Eurasian Basin. The mean age of the bottom waters in the Eurasia Basin is less than 40 years. On passing across the Lomonosov Ridge, the mean bottom water age increases to 70 years in the Makarov Basin and further to 260 years in the Canada Basin. In oceanic basins where the circulation is significantly blocked by sills, the maximum tracer age can be more useful for describing the ventilation features. The steep meridional gradient in the tracer age maximum below a depth of 500 m is attributed to the Lomonosov Ridge, which divides the Arctic Ocean into two basins with different age properties. Typically, the latitude–depth section of zonal maximum samples the older waters in the Amerasian part, whereas the zonal minimum represents the young age water in the Eurasia Basin. The maximum age of bottom waters in the Eurasia, Makarov and Canada basins are 50, 100 and 280 years, respectively. Interestingly, the difference between the maximum and minimum tracer ages tends to be small in the bottom parts in all sub-basins. This indicates the presence of strong horizontal mixing processes near the bottom. Note that also in the present-day Arctic Ocean there are strong property gradients in the deep water across the Lomonosov Ridge. In the Amerasian Basin the oxygen content is lower and age inferred from tracers is older than in the Eurasian Basin (e.g., Tanhua et al. 2009; Björk et al. 2010).
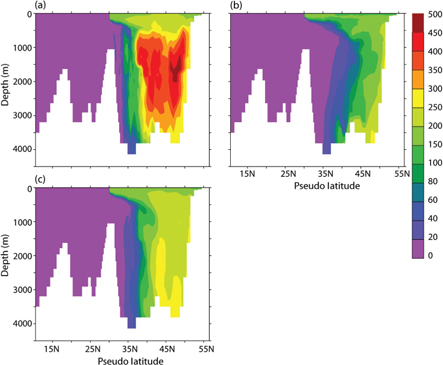
Fig. 10
The tracer age from the model (a) zonal maximum, (b) zonal minimum and (c) zonal average. The latitude corresponds to the remapped model grid. The bottom topography represents the maximum depth of ocean for the corresponding latitude.
The frequency function χ for age distribution in the Arctic Ocean and frequency function φ for transit time in the middle of Fram Strait are depicted in Fig. 11, which shows the time mean of these quantities at steady state. The age distribution is characterized by a bimodal distribution pattern with a smaller peak at very young ages (<50 years) and a larger peak at about 210 years. This larger peak arises from diffusive mixing of young (<100 years) and old (>200 years) water. Geographically, this mixing occurs primarily near the Lomonosov Ridge and in Fram Strait where there are sharp gradients in tracer age. After the main peak, the age distribution tends gradually to zero, having a long tail extending to very high ages, reflecting the relatively isolated water in the Amerasia Basin
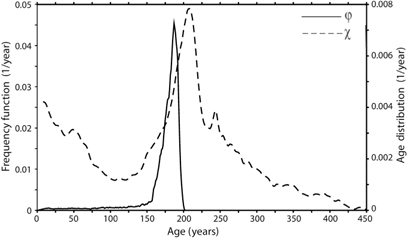
Fig. 11
The frequency function for the age distribution of particles in the Miocene Arctic Ocean, χ (dashed line) and the frequency function for the particles leaving the Arctic Ocean, φ (continuous line). The left y axis is for φ and right y axis is for χ.
The frequency function φ of water leaving the Arctic Ocean has a unimodal distribution. Since the outflow takes place only in the upper ocean, the frequency function φ tends to peak at the mean age of water in the upper layer. However, due to the diffusive mixing of the age tracer, the turnover time implied by φ, on the order of 200 years, is significantly shorter than the flow-based turnover time computed from Eqn. 4, which is on the order of 500 years. It should be noted that due to the diffusive mixing, the theoretical non-diffusive relation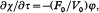 
derived by Bolin & Rodhe (1973), does not apply to our simulation. The narrow peak of φ seems to suggest that there is primarily a “pipe-like” flow through the basin (Bolin & Rohde 1973; Björkström 1978). In the absence of mixing, the zero age water entering the Arctic Ocean would gradually become older and essentially the oldest water would be exiting to the North Atlantic Ocean. Such an exchange-flow pattern was obtained by Thompson et al. (2010) in their idealized basin with narrow strait width (96 km). In the present simulation, the narrowly-peaked age distribution of the outflowing water may reflect strong diffusive mixing of the age tracer in the strait region rather than a pipe-like flow through the basin. We note, however, that the turnover time (ca. 500 years) is larger than the mean age of the basin water (ca. 200 years), which is a typical feature for pipe-like exchange flows (Bolin & Rodhe 1973; Thompson et al. 2010).
As a final point, we comment briefly on how the ventilation time scales depend on the basin volume, using results obtained by Thompson et al. (2010). Their idealized bowl-shaped basin has a depth that is comparable to the one in our Miocene simulation, but the basin area and volume are about 10 times smaller. If the exchange flow through the strait would be similar in the simulations, then the turnover time would be 10 times larger in the present simulation. By invoking the classical thermocline scaling, however, Thompson et al. (2010) proposed that the exchange flow should be proportional to the square root of the basin area. This roughly suggests a threefold increase of the exchange flow through Fram Strait in our simulation with the Miocene bathymetry. The turnover time, which is the ratio of basin volume to the net exchange flow, should accordingly also increase by about a factor of three. Here, we find that the turnover time is increased by about a factor of six compared to Thompson et al. (2010), implying some strengthening of the exchange flow with increasing basin area. However, the exchange-flow increase in the present experiment is weaker (by roughly a factor of 2) than expected form the classical thermocline scaling. Interestingly, the mean age in the present simulations is about a factor of three greater than in Thompson et al. (2010), seemingly in accordance with the classical thermocline scaling. A tentative explanation for the departures from the simple scaling proposed by Thompson et al. (2010) is that the presence of sub-basins and ridges affect the ventilation features, making it difficult to obtain information on the volume dependence by comparing our results and those of Thompson et al. (2010).
Discussion and conclusion
The tectonic opening of Fram Strait through seafloor spreading (Engen et al. 2008), enhancing the water exchange between the Arctic and Atlantic oceans during early Miocene, was a significant climatic event that strongly influenced the paleoceanographic conditions in the Arctic Ocean and possibly affected the global thermohaline circulation (e.g., Haley et al. 2008). The evolution of the Arctic Ocean to a fully ventilated “ocean stage”, as suggested by the ACEX core analyses, has indeed been attributed to the opening of Fram Strait (Jakobsson et al. 2007). The dimensions of Fram Strait and the climatic boundary conditions should have been critical in determining the ventilation time scale and thereby the oxygen content of the sub-surface waters in the palaeo Arctic Ocean (Jakobsson et al. 2007; Thompson et al. 2010). In the present paper, a qualitative analysis of the ventilation time and distribution of water age in the Miocene Arctic Ocean has been undertaken using an ocean circulation model. The model simulation uses a palaeo-bathymetric reconstruction for the early Miocene Arctic Ocean, which is believed to broadly capture the main bathymetric features, such as sills and different sub-basins, although the reconstruction is indeed based on a sparse geologic and geophysical database (Jakobsson et al. 2007). The physical forcing of the ocean model is drastically simplified and accounts only for the net freshwater input to the Arctic Basin. The simulated Arctic Ocean stratification has essentially a two-layer structure and hence lacks a counterpart to the intermediate Atlantic Water layer, which is present in the modern Arctic Ocean (e.g., Rudels 1995). A two-layer like stratification in the early Miocene Arctic is consistent with the notion that the sea ice formation was likely too weak to sustain the cold but less saline bottom layer, which presently is encountered below the intermediate Atlantic layer. The model is integrated with a passive age tracer, which is taken as a rough indicator of the oxygen content below the surface layer.
The modelled surface circulation shows some resemblance to the modern Arctic Ocean circulation. In particular, the modelled surface circulation in the Canadian Basin has similarities with the cyclonic circulation regime that prevails at times in the Beaufort Gyre (e.g., Proshutinsky et al. 2002). However, given the absence of wind forcing and surface heat fluxes, the details of the simulated surface circulation should be interpreted with great care. The exchange flow in Fram Strait has a two-layer structure with a low salinity outflow from the Arctic confined to a relatively thin upper layer and a saline inflow from the North Atlantic below. We note that a global climate model simulation of the Miocene which used a bathymetry similar to ours, but a coarser resolution, also yielded a two-layer like stratification in the Arctic Ocean and a similar flow structure through Fram Strait (Herold et al. 2012). The occurrence of similar circulation patterns in climate model and present process-oriented model further strengthen the notion that the Arctic Ocean circulation during early Miocene was dominated by salinity variations and primarily forced by the freshwater flux. Most likely, the absence of wind forcing causes our simulated time-mean circulation to resemble the present-day cyclonic circulation regime, which prevails during boreal summer when the winds are generally weak and preferentially cyclonic. The Miocene simulation exhibits some internal circulation variability, which is associated with baroclinic eddies. However, the variability produced by our model does not yield patterns resembling the present-day anticyclonic circulation regime, which prevails during boreal winter when the winds are stronger and preferentially anticyclonic.
The turnover time can be considered as a first-order estimate of the mean age of the water in an ocean basin (Jakobsson et al. 2007; Thompson et al. 2010). Based on simulations with idealized bathymetry, Thompson et al. 2010 found that the turnover time is greater than the mean water age for strait widths of about 100 km or smaller; for a 325 km wide strait, the reverse is true. The width of Fram Strait in our bathymetric reconstruction of the early Miocene Arctic Ocean is about 100 km. Consistent with this; the turnover time and mean tracer age are 480 and 180 years, respectively, in the present simulation. This suggests a “pipe-like” exchange circulation in the simulation, characterized by the water exiting Fram Strait being considerably older than mean age of the water in the basin (Bolin & Rodhe 1973; Thompson et al. 2010). The frequency function for age distribution is distinguished by a bimodal distribution pattern with a primary peak at very young age (<50 years) and secondary larger peak at relatively old age (ca. 210 years). This larger peak in the age distribution arises due to strong diffusive mixing of the age tracer, primarily occurring near the Lomonosov Ridge where there is a sharp gradient in age between the relatively young Eurasian Basin water and the older Amerasian Basin water. The age of oldest water in the early Miocene Arctic Ocean is 475 years in our simulation.
The turnover time and tracer age are potentially sensitive to surface wind forcing and ensuing wind-driven circulation. In general, the surface winds enhance the oceanic circulation, suggesting that the present simulation, conducted in the absence of wind forcing, should yield upper bounds on the ventilation time scales. Thompson et al. (2010) carried out experiments to test the sensitivity of the ventilation features to wind-forced exchange flow through the strait. When a cyclonic wind stress pattern of an amplitude of about 0.1 N/m2 was applied over the basin, a typical value for present-day Arctic Ocean and Nordic seas (Risien & Chelton 2006), the maximum tracer age was reduced by 60% and the mean tracer age and turnover time by 40% (compared to the case without wind forcing). Assuming that the results of Thompson et al. (2010) also hold approximately for the present larger and topographically more complicated basin, the turnover time and mean tracer age should decrease to about 300 and 100 years, respectively, in the presence of a similar wind forcing. In fact, this “wind-reduced” turnover time is comparable to the 250-year turnover time suggested by Jakobsson et al. (2007) to yield full oxygenation of the early Miocene Arctic Ocean.
It is interesting to note that although Fram Strait is fairly narrow and shallow in the present early Miocene simulation (which has no counterparts to Bering Strait and the Barents Sea and furthermore is conducted in the absence of wind forcing), the resulting bulk ventilation timescales appear to be comparable to or shorter than corresponding estimates based on chemical tracer studies in the present-day Arctic Ocean (e.g., Schlosser et al. 1997; Tanhua et al. 2009). However, a more detailed comparison with the observationally-based estimates due to Tanhua et al. (2009) reveal that our modelled age is much larger in the upper 1000 m. Below about 1500 m, in contrast, the model results and the observationally-based estimates are of comparable magnitudes. In the present-day Arctic Ocean, the Atlantic Water circulation efficiently flushes the intermediate depths. This circulation is partly driven remotely by wind-forcing over the Nordic seas (Nøst & Isachsen 2003). Below the intermediate Atlantic Water layer, the ventilation of the Arctic Ocean is accomplished by injection of dense brine-enriched shelf waters and inflow through Fram Strait of deep water formed in the Nordic seas (e.g., Rudels 1995; Rudels et al. 2005). Therefore, when comparing the ventilation features one has to remember that the present-day Arctic Ocean has a fairly complicated three-layer stratification and that its circulation is partly wind-driven, whereas our model, which lacks wind-forcing and oceanic temperature variations, yields a two-layer stratification.
Despite the fact that present study is highly idealized and associated with several uncertainties, it nevertheless suggests that an estuarine circulation in the early Miocene Arctic Ocean could have renewed the deep waters at a rate that is comparable to the renewal time in the modern Arctic Ocean; although the ventilation mechanism is quite different in the model of the early Miocene Arctic Ocean. By further assuming that the present-day Arctic Ocean relationship between water age and subsurface oxygen content (e.g., Tanhua et al. 2009; Björk et al. 2010) applied also in the early Miocene Arctic Ocean, our simulation give support the notion of Jakobsson et al. (2007) that the transition to oxygenated conditions documented in the ACEX core was caused by a strengthening of a salinity-dominated estuarine circulation.
Our model experiments suggest that strong spatial water mass age gradients prevailed in the early Miocene at the ACEX coring sites on the Lomonosov Ridge crest. In addition, the sites’ palaeo-ocean depths were likely substantially shallower than at present (O'Regan et al. 2008). Careful attention should therefore be given while interpreting the palaeo proxies for oxygen content in the ACEX sediment record as a representative of the entire early Miocene Arctic Ocean.
However, the distribution of model tracer ages (Figs. 9 and 10) implies that though the model excludes the effects wind forcing, the ventilation time is relatively close to the observational estimates of water mass age in the modern Arctic Ocean. Below the thin surface mixed layer (250 m in our study) the ventilation has been accomplished most likely due to the inflow of fully ventilated water from the Atlantic Ocean during the early Miocene period. Thus, the exchange flow through Fram Strait became vital in determining the ventilation timescale of intermediate and deep water in the Miocene Arctic Ocean. Finally, with a width of 100 km and sill depth of 1000 m a ventilated Arctic Ocean was achieved in our simulation implying that the first signs of ventilation in the ACEX drill core from the Lomonosov Ridge may occur earlier in time than seafloor spreading fully connected the Arctic Ocean with the North Atlantic through the Lena Trough.
Acknowledgements
This work was supported by the Bert Bolin Centre for Climate Research, Stockholm University, Sweden. The model integration were done in the Linux cluster “Tornado” at the National Supercomputer Centre in Sweden and the support from centre's staff is acknowledged. Figures were drawn using Ferret, Matlab and the GIS software Geomedia Professional.
References
Backman
J.
&
Moran
K. 2009.
Expanding the Cenozoic paleoceanographic record in the central Arctic Ocean: IODP Expedition 302 synthesis. Central European Journal of Geosciences 1,
157–175.
[Crossref]
Backman
J.,
Moran
K.,
McInroy
L.A.,
Mayer
D.B.
& the Expedition 302 Scientists 2006. Expedition 302 summary. In: Proceedings of the Integrated Ocean Drilling Program 302.
College Station,
TX: Integrated Ocean Drilling Program Management International.
Björk
G.,
Anderson
L.G.,
Jakobsson
M.,
Antony
D.,
Eriksson
B.,
Eriksson
P.B.,
Hell
B.,
Hjalmarsson
S.,
Janzen
T.,
Jutterström
S.,
Linders
J.,
Löwemark
L.,
Marcussen
C.,
Olsson
K.A.,
Rudels
B.,
Sellén
E.
&
Sølvsten
M. 2010.
Flow of Canadian Basin deep water in the western Eurasian Basin of the Arctic Ocean. Deep Sea Research Part I 57,
577–586.
[Crossref]
Björk
G.,
Jakobsson
M.,
Rudels
B.,
Swift
J.H.,
Anderson
L.,
Darby
D.A.,
Backman
J.,
Coakley
B.,
Winsor
P.,
Polyakov
L.
&
Edwards
M. 2007.
Bathymetry and deep-water exchange across the central Lomonosov Ridge at 88° – 89°N. Deep-Sea Research Part I 54,
1197–1208.
[Crossref]
Björkström
A. 1978.
A note on the relation between average age and average transit time in natural reservoirs. Tellus 30,
185–188.
[Crossref]
Bolin
B.
&
Rodhe
H. 1973.
A note on the concepts of age distribution and residence time in natural reservoirs. Tellus 25,
58–62.
[Crossref]
Brinkhuis
H.,
Schouten
S.,
Collinson
M.E.,
Sluijs
A.,
Sinninghe Damsté
J.S.,
Dickens
G.R.,
Huber
M.,
Cronin
T.M.,
Onodera
J.,
Takahashi
K.,
Bujak
J.P.,
Stein
R.,
van der Burgh
J.,
Eldrett
J.S.,
Harding
I.C.,
Lotter
A.F.,
Sangiorgi
F.,
van Konijnenburg-van Cittert
H.,
de Leeuw
J.W.,
Matthiessen
J.,
Backman
J.,
Moran
K.
& the Expedition 302 Scientists
2006. Episodic fresh surface waters in the Eocene Arctic Ocean. Nature 441, 606–609.
[Crossref]
Colella
P.
&
Woodward
P.R. 1984.
The piecewise parabloic method (PPM) for gas-dynamical simulations. Journal of Computational Physics 54,
174–201.
[Crossref]
Cox
M.D. 1989.
An idealized model of the World ocean. Part I: the global scale water masses. Journal of Physical Oceanography 19,
1730–1752.
[Crossref]
Darby
D.A.
2008. Arctic perennial ice cover over the last 14 million years. Paleoceanography
23, PA1S07. doi: 10.1029/2007PA001479.
[Crossref]
Deleersnijder
E.,
Campin
J.M.
&
Delhez
E.J.M. 2001.
The concept of age in marine modelling: I. Theory and preliminary model results. Journal of Marine Systems 28,
229–267.
[Crossref]
Deleersnijder
E.,
Mouchet
A.,
Delhez
E.J.M.
&
Beckers
J.M. 2002.
Transient behaviour of water ages in the World Ocean. Mathematical and Computer Modelling 36,
121–127.
[Crossref]
Döös
K.,
Nycander
J.
&
Coward
A.C.
2008. Lagrangian decomposition of the Deacon Cell. Journal of Geophysical Research—Oceans
113, article no. C07028, doi: 10.1029/2007JC004351.
[Crossref]
Engen
Ø.,
Faleide
J.I.
&
Dyreng
T.K. 2008.
Opening of the Fram Strait gateway: a review of plate tectonic constraints. Tectonophysics 450,
51–69.
[Crossref]
England
M.H. 1995.
The age of water and ventilation time-scales in a global ocean model. Journal of Physical Oceanography 25,
2756–2777.
[Crossref]
Garcia-Castellanos
D.,
Estrada
F.,
Jiménez-Munt
I.,
Gorini
C.,
Fernàndez
M.,
Vergés
J.
&
De Vicente
R. 2009.
Catastrophic flood of the Mediterranean after the Messinian salinity crisis. Nature 462,
778–781.
[Crossref]
Gent
P.R.
&
McWilliams
J.C. 1990.
Isopycnal mixing in ocean circulation models. Journal of Physical Oceanography 20,
150–155.
[Crossref]
Gladenkov
A.Y.,
Oleinik
A.E.,
Marincovich
Jr. L.
&
Barinov
K.B. 2002.
A refined age for the earliest opening of the Bering Strait. Palaeogeography, Palaeoclimatology, Palaeoecology 183,
321–328.
[Crossref]
Griffies
S.M.
2007. Elements of MOM4p1. GFDL Ocean Group Technical Report 6. Princeton, NJ: Geophysical Fluid Dynamics Laboratory, National Oceanic and Atmospheric Administration.
Griffies
S.M.
&
Hallberg
R.W. 2000.
Biharmonic friction with a Smagorisky viscosity for use in large-scale eddy-permitting ocean models. Monthly Weather Review 128,
2935–2946.
[Crossref]
Haley
B.A.,
Frank
M.,
Spielhagen
R.F.
&
Eisenhauer
A. 2008.
Influence of brine formation on Arctic Ocean circulation over the past 15 million years. Nature Geoscience 1,
68–72.
[Crossref]
Held
I.M.
&
Soden
B.J. 2006.
Robust response of the hydrological cycle to global warming. Journal of Climate 19,
5686–5699.
[Crossref]
Herold
N.,
Huber
M.,
Müller
R.D.
&
Seton
M.
2012. Modelling the Miocene climatic optimum. Part 2: ocean circulation, Paleoceanography. Paleoceanography, doi: 10.1029/2010PA002041.
[Crossref]
Hickey
L.J.,
Johnson
K.R.
&
Dawson
M.R. 1988.
The stratigraphy, sedimentology and fossils of the Haughton Formation: a post-impact crater fill, Devon Islands, N.W.T., Canada. Meteoritics 23,
221–231.
Jakobsson
M.,
Backman
J.,
Rudels
B.,
Nycander
J.,
Frank
M.,
Mayer
L.,
Jokat
W.,
Sangiorgi
F.,
Brinkhuis
H.,
King
J.
&
Moran
K. 2007.
The early Miocene onset of a ventilated circulation regime in the Arctic Ocean. Nature 447,
986–990.
[Crossref]
Jakobsson
M.,
Macnab
R.,
Mayer
L.,
Anderson
R.,
Edwards
M.,
Hatzky
J.,
Schenke
H.W.
&
Johnson
P.
2008. An improved bathymetric portrayal of the Arctic Ocean: implications for ocean modeling and geological, geophysical and oceanographic analyses. Geophysical Research Letters
35, L07602, doi: 10.1029/2008GL033520.
[Crossref]
Jönsson
B.,
Lundberg
P.
&
Döös
K. 2004.
Baltic sub-basin turnover times examined using the Rossby Centre Ocean Model. Ambio 33,
257–260.
Klenke
M.
&
Schenke
H.W. 2002.
A new bathymetric model for the central Fram Strait. Marine Geophysical Researches 23,
367–378.
[Crossref]
Krijgsman
W.,
Hilgen
F.J.,
Raffi
I.,
Sierro
F.J.
&
Wilson
D.S. 1999.
Chronology, causes and progression of the Messinian salinity crisis. Nature 400,
652–655.
[Crossref]
Krylov
A.A.,
Andreeva
I.A.,
Vogt
C.,
Backman
J.,
Krupskaya
V.V.,
Grikurov
G.E.,
Moran
K.
&
Shoji
H.
2008. A shift in heavy and clay mineral provenance indicates a middle Miocene onset of a perennial sea ice cover in the Arctic Ocean. Paleoceanography
23, PA1S06, doi: 10.1029/2007PA001497.
[Crossref]
Large
W.G.,
McWilliams
J.C.
&
Doney
S.C. 1994.
Oceanic vertical mixing: a review and a model with a nonlocal boundary layer parameterization. Reviews of Geophysics 32,
363–403.
[Crossref]
McNeil
D.H. 1989. Foraminiferal zonation and biofacies analysis of Cenozoic strata in the Beaufort–Mackenzie Basin of Arctic Canada. In: Current Research, Part G, Geological Survey of Canada Paper 89-1G. Pp. 203–223.
Ottawa: Geological Survey of Canada.
Merryfield
W.J.
&
Holloway
G. 2003.
Application of an accurate advection algorithm to sea-ice modelling. Ocean Modelling 5,
1–15.
[Crossref]
Moran
K.,
Backman
J.,
Brinkhuis
H.,
Clemens
S.C.,
Cronin
T.,
Dickens
G.R.,
Eynaud
F.,
Gattacceca
J.,
Jakobsson
M.,
Jordan
R.W.,
Kaminski
M.,
King
J.,
Koc
N.,
Krylov
A.,
Martinez
N.,
Matthiessen
J.,
McInroy
D.,
Moore
T.C.,
Onodera
J.,
O'Regan
M.,
Pälike
H.,
Rea
B.,
Rio
D.,
Sakamoto
T.,
Smith
D.C.,
Stein
R.,
St John
K.,
Suto
I.,
Suzuki
N.,
Takahashi
K.,
Watanabe
M.,
Yamamoto
M.,
Farrell
J.,
Frank
M.,
Kubik
P.,
Jokat
W.
&
Kristoffersen
Y. 2006.
The Cenozoic palaeoenvironment of the Arctic Ocean. Nature 441,
601–605.
[Crossref]
Nilsson
J.
&
Walin
G. 2010.
Salinity-dominated thermohaline circulation in sill basins: can two stable equilibria exist? Tellus Series A 62,
123–133.
[Crossref]
Nilsson
J.,
Walin
G.
&
Broström
G. 2005.
Thermohaline circulation induced by bottom friction in sloping-boundary basins. Journal of Marine Research 63,
705–728.
[Crossref]
Nøst
O.A.
&
Isachsen
P.E. 2003.
The large-scale time-mean ocean circulation in the Nordic seas and Arctic Ocean estimated from simplified dynamics. Journal of Marine Research 61,
175–210.
[Crossref]
O'Regan
M.,
Moran
K.,
Backman
J.,
Jakobsson
M.,
Sangiorgi
F.,
Brinkhuis
H.,
Pockalny
R.,
Skelton
A.,
Stickley
C.,
Koc
N.,
Brumsack
H.-J.
&
Willard
D.
2008. Mid-Cenozoic tectonic and paleoenvironmental setting of the central Arctic Ocean. Paleoceanography
23, PA1S20, doi: 10.1029/2007PA001559.
[Crossref]
O'Regan
M.,
Williams
C.J.,
Frey
K.E.
&
Jakobsson
M. 2011.
A synthesis of the long-term paleoclimatic evolution of the Arctic. Oceanography 24(3),
66–80.
[Crossref]
Pagani
M.,
Pedentchouk
N.,
Huber
M.,
Sluijs
A.,
Schouten
S.,
Brinkhuis
H.,
Damsté
J.S.,
Dickens
G.R.
& the Expedition 302 Scientists
2006. Arctic hydrology during global warming at the Palaeocene/Eocene thermal maximum. Nature 442, 671–675.
[Crossref]
Prather
M. 1986.
Numerical advection by conservation of second-order moments. Journal of Geophysical Research—Atmospheres 91,
6671–6681.
[Crossref]
Pratt
L.J.
&
Spall
M.A. 2008.
Circulation and exchange in choked marginal seas. Journal of Physical Oceanography 38,
2639–2661.
[Crossref]
Proshutinsky
A.,
Bourke
R.H.
&
McLaughlin
F.A.
2002. The role of the Beaufort Gyre in Arctic climate variability: seasonal to decadal climate scales. Geophysical Research Letters
29, article no. 2100, doi: 10.1029/2002GL015847.
[Crossref]
Risien
C.M.
&
Chelton
D.B. 2006.
A satellite derived climatology of global ocean winds. Remote Sensing of Environment 105,
221–236.
[Crossref]
Rudels
B. 1995.
The thermohaline circulation of the Arctic Ocean and the Greenland Sea. Philosophical Transactions: Physical Sciences and Engineering 352,
287–299.
[Crossref]
Rudels
B.,
Björk
G.,
Nilsson
J.,
Winsor
P.,
Lake
I.
&
Nohr
C. 2005.
The interaction between waters from the Arctic Ocean and the Nordic seas north of Fram Strait and along the East Greenland Current: results from the Arctic Ocean-02 Oden expedition. Journal of Marine Systems 55,
1–30.
[Crossref]
Schlosser
P.,
Kromer
B.,
Ekwurzel
B.,
Bönisch
G.,
McNichol
A.,
Schneider
R.,
von Reden
K.,
Östlund
H.G.
&
Swift
J.H. 1997.
The first trans-Arctic 14C section: comparison of the mean ages of the deep waters in the Eurasian and Canadian basins of the Arctic Ocean. Nuclear Instruments and Methods in Physics Research Section B 123,
431–437.
[Crossref]
Sluijs
A.,
Schouten
S.,
Pagani
M.,
Woltering
M.,
Brinkhuis
H.,
Sinninghe Damsté
J.S.,
Dickens
G.R.,
Huber
M.,
Reichart
G.J.,
Stein
R.,
Matthiessen
J.,
Lourens
L.J.,
Pedentchouk
N.,
Backman
J.,
Moran
K.
& the Expedition 302 Scientists
2006. Subtropical Arctic Ocean temperatures during the Palaeocene/Eocene thermal maximum. Nature 441, 613.
Spall
M.A. 2005.
Buoyancy-forced circulations in shallow marginal seas. Journal of Marine Research 63,
729–752.
[Crossref]
Steele
M.,
Ermold
W.,
Hakkinen
S.,
Holland
D.,
Holloway
G.,
Karcher
M.,
Kauker
F.,
Maslowski
W.
&
Steiner
N. 2001.
Adrift in the Beaufort Gyre: a model intercomparison. Geophysical Research Letters 28,
2935–2938.
[Crossref]
Tanhua
T.,
Jones
E.P.,
Jeansson
E.,
Jutterström
S.,
Smethie
Jr. W.M.,
Wallace
D.W.R.
&
Anderson
L.G.
2009. Ventilation of the Arctic Ocean: mean ages and inventories of anthropogenic CO2 and CFC-11. Journal of Geophysical Research—Oceans
114, C01002. doi: 10.1029/2008JC004868.
[Crossref]
Thompson
B.,
Nilsson
J.,
Nycander
J.,
Jakobsson
M.
&
Döös
K.
2010. Ventilation of the Miocene Arctic Ocean: an idealized model study. Paleoceanography, PA4216. doi: 10.1029/2009PA001883.
[Crossref]
Timmermans
M.-L.,
Winsor
P.
&
Whitehead
J.A. 2005.
Deep-water flow over the Lomonosov Ridge in the Arctic Ocean. Journal of Physical Oceanography 35,
1489–1493.
[Crossref]
Torsvik
T.H.,
Carlos
D.,
Mosar
J.,
Mosar
J.,
Robin
L.,
Cocks
M.
&
Malme
T.N.
2002.
Global reconstructions and North Atlantic paleogeography 400 Ma to Recent.
In E.A. Eide (ed.): BATLAS. Mid Norway plate reconstructions atlas with global and Atlantic perspectives. Pp. 18–39. Trondheim: Geological Survey of Norway.
Verhoeven
K.,
Louwye
S.,
Eiríksson
J.
&
De Schepper
S. 2011.
A new age model for the Pliocene–Pleistocene Tjörnes section on Iceland: its implication for the timing of North Atlantic–Pacific palaeoceanographic pathways. Palaeogeography, Palaeoclimatology, Palaeoecology 309,
33–52.
[Crossref]
von der Heydt
A.
&
Dijkstra
H.A.
2006. Effect of ocean gateways on the global ocean circulation in the late Oligocene and early Miocene. Paleoceanography
21, PA1011, doi: 10.1029/2005PA001149.
[Crossref]
Waddell
L.M.
&
Moore
T.C.
2008. Salinity of the Eocene Arctic Ocean from oxygen isotope analysis of fish bone carbonate. Paleoceanography
23, PA1S12, doi: 10.1029/2007PA001451.
[Crossref]
White
J.M.
&
Ager
T.A. 1994.
Palynology, paleoclimatology and correlation of middle Miocene beds from Porcupine River (Locality 90-1) Alaska. Quaternary International 22/23,
43–77.
[Crossref]
Zachos
J.,
Pagani
M.,
Sloan
L.,
Thomas
E.
&
Billups
K. 2001.
Trends, rhythms and aberrations in global climate 65 Ma to present. Science 292,
686–693.
[Crossref]