RESEARCH ARTICLE
Atmospheric controlled freshwater release at the Laptev Sea continental margin
Dorothea Bauch1,
Matthias Gröger2,
Igor Dmitrenko1,
Jens Hölemann3,
Sergey Kirillov4,
Andreas Mackensen3,
Ekatarina Taldenkova5 &
Nils Andersen6
1Leibniz Institute of Marine Sciences, Kiel University, Wischhofstrasse 1–3, DE-24148, Kiel, Germany; 2Max Planck Institute for Meteorology, Bundesstrasse 53, DE-20146, Hamburg, Germany; 3Alfred Wegener Institute for Polar and Marine Research, Am Handelshafen 12, DE-27570, Bremerhaven, Germany; 4Arctic and Antarctic Research Institute, 38 Bering Street, RU-199397, St. Petersburg, Russian Federation; 5Lomonosov Moscow State University, GSP-1, Leninskie Gory, RU-119991, Moscow, Russian Federation; 6Leibniz Laboratory for Radiometric Dating and Stable Isotope Research, Kiel University, Max-Eyth-Strasse 11–13, DE-24118, Kiel, Germany
Abstract
Considerable interannual differences were observed in river water and sea-ice meltwater inventory values derived from δ18O and salinity data in the Eurasian Basin along the continental margin of the Laptev Sea in the summers of 1993 and 1995, and in the summers of 2005 and 2006 during Nansen and Amundsen Basins Observational system (NABOS) expeditions. The annually different pattern in river and sea-ice meltwater inventories remain closely linked for all of the years studied, which indicates that source regions and transport mechanisms for both river water and sea-ice formation are largely similar over the relatively shallow Laptev Sea Shelf. A simple Ekman trajectory model for surface Lagrangian particles based solely on wind forcing can explain the main features observed between years with significantly different wind patterns and vorticities, and can also explain differences in river water distributions observed for years with a generally similar offshore wind setting. An index based on this simplified trajectory model is rather similar to the vorticity index, but reflects the hydrology on the shelf better for distinctive years. This index is not correlated with the Arctic Oscillation, but rather with a local mode of oscillation, which controls the outflow and distribution of the Eurasian Basin major freshwater source on an annual timescale.
Keywords:
Arctic Ocean halocline;
atmospheric forcing;
Laptev Sea;
stable isotopes;
water masses.
Correspondence
Dorothea Bauch, Leibniz Institute of Marine Sciences, Kiel University,Wischhofstrasse 1–3, DE-24148 Kiel. Germany. Email: dbauch@ifm-geomar.de
Published: 1 January 2011
Citation: Polar Research 2011, 30: 5858 - DOI: 10.3402/polar.v30i0.5858
Polar Research 2011. © 2011 D. Bauch et al. This is an open access article distributed under the terms of the Creative Commons Attribution-Noncommercial 3.0 Unported License (http://creativecommons.org/licenses/by-nc/3.0/), permitting all non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Water masses from the shelf areas are an important contribution to the Arctic Ocean halocline. Understanding the processes and the exchange of water masses between the Arctic Ocean Basin and the shelf areas is important with respect to halocline stability. A weaker halocline may impede sea-ice formation and enhance the heat flux of the ocean atmosphere, feeding back positively on Arctic climate warming. Summer salinity trends recorded on several Siberian Shelf seas indicate a close relationship with winter Arctic Oscillation (AO) and North Atlantic Oscillation (NAO) indices on decadal timescales (Steele & Ermold
2004). During the positive phase of the AO/NAO, moisture-carrying storm tracks penetrate farther towards northern Eurasia, thereby increasing the potential for precipitation and enhanced river discharge during the subsequent warm season. Analysis of the freshwater content and its anomalies in the Laptev and East Siberian seas reveals a considerable freshwater storage and movement between the two areas correlated with atmospheric forcing (Dmitrenko et al.
2008). Observations have shown that the summer atmospheric circulation pattern in the region can strongly influence the contribution of river water to the halocline of the Arctic Ocean (e.g., Guay et al.
2001; Dmitrenko et al.
2005), and it is generally assumed that low salinity surface waters from the Laptev Sea may be transported either northwards across the shallow shelf into to the Arctic Ocean interior, or may be spread eastwards and enter it within the Canadian part of the basin (Guay et al.
2001; Dmitrenko et al.
2005; Dmitrenko et al.
2008). Model results also imply that the atmospheric forcing governs the direction of freshwater transport in the Laptev Sea (Johnson & Polyakov
2001). Variations in residence times of Laptev Sea waters may significantly influence the structure of the halocline in the Arctic Ocean (Johnson & Polyakov
2001), and may also correspond with different prevailing wind-forced circulations (Proshutinsky & Johnson
1997).
We use stable oxygen δ18O isotopes of the water to study the exchange of water masses between the Arctic Ocean Basin and the shelf areas. The vast Siberian Shelf areas are significantly influenced by river run-off and sea-ice processes, and δ18O is an ideal tracer to distinguish between these different freshwater sources (Bauch et al.
2003; Bauch et al.
2005). Within the Laptev Sea, winter sea-ice formation dominates over sea-ice melting during summer, and brine-enriched waters have been shown to move similarly to river water in response to atmospheric forcing (Bauch, Dmitrenko, Wegner et al.
2009). Inventories of river water and sea-ice meltwater calculated for stations at the Laptev Sea continental slope for 1993, 1995, 2005 and 2006 show considerable interannual variation. The vorticity index has been used to characterize the atmospheric forcing on the Laptev Sea surface waters basin (Dmitrenko et al.
2005). The vorticity index defined by Walsh et al. (1996) generalizes sea level pressure (SLP) for an area within a radius of 550 km of 85°N and 125°E, a region located in the Arctic Ocean to the north of the Laptev Sea, and is calculated as the numerator of the finite-difference Laplacian of SLP data from June to September. Because the vorticity index for some years does not adequately reflect the hydrological setting in the Laptev Sea, we use a simple numerical Ekman drift trajectory model to investigate the effect of near surface winds on the distribution of river water off the shelf break.
Database and methods
Samples were collected during NABOS expeditions in September 2005 and 2006 (Fig. 1). Oxygen isotopes for 2005 were analysed at the Stable Isotope Laboratory of the Alfred Wegener Institute in Bremerhaven (Mackensen
2001). Oxygen isotopes for 2006 were analysed at the Leibniz Laboratory for Radiometric Dating and Stable Isotope Research in Kiel, applying the CO2 water isotope equilibration technique on at least two subsamples on a Thermo Finnigan Gas Bench II unit, coupled to a Thermo Finnigan DeltaPlus XL mass spectrometer (Thermo Fisher Scientific, Waltham, MA, USA). The overall measurement precision for all δ18O analysis is ±0.03‰ or smaller. The 18O/16O ratio is given versus the Vienna Standard Mean Ocean Water in the usual d-notation (Craig
1961). Additional data are available from the literature (Schmidt et al.
1999), and were collected at the Laptev Sea continental slope during expeditions of the RV Polarstern in September 1993 and 1995 (Fig. 1; Frank
1996). The measurement precision for these data is ±0.03‰ or smaller in δ18O.
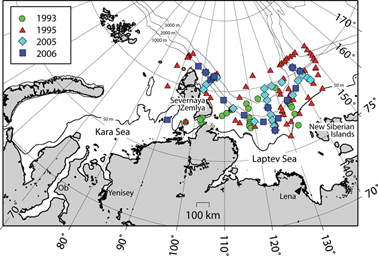
Fig. 1
Geographical distribution of stations with δ18O data from summer expeditions in 1993, 1995, 2005 and 2006. Also indicated are the Ob and Yenisey rivers in the Kara Sea and the Lena River in the Laptev Sea (an arrowhead marks the major discharge in the Lena Delta).
In line with previous tracer studies we relate interannual variations in freshwater distribution to corresponding differences in the forcing wind pattern (e.g., Guay et al.
2001). However, we do not restrict this to a visual comparison with smoothed monthly mean wind fields to infer the influence of surface winds for the freshwater distribution on the Laptev Shelf. Instead, we provide a more reliable semi-quantitative numerical trajectory approach, which more accurately considers the spatiotemporal variability of surface winds. Our trajectory approach formulates the atmosphere–ocean momentum transfer using a fraction f of the 10-m wind field velocities, and calculates the drift X of Lagrangian particles according to the formula:
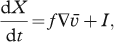
where 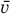 is the particle velocity and I is an inertia term
is the particle velocity and I is an inertia term
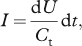
with the velocity change dU and an inertial time constant Ct, which is set to 30 days. The inclusion of the latter term smoothes the unrealistic jumps of particles resulting from sudden hard changes in wind direction. Furthermore, an Ekman deviation of 45° to the right from the wind vector is applied. Hence, the model misses the pressure-driven and depth-varying circulation, and instead focuses on Ekman stresses applied by the atmosphere. Small-scale features like plume dynamics near the coast (e.g., Yankovsky & Chapman
1997; Chapman & Lentz
2005) or near special topographic structures (Gawarkiewicz et al.
1995) are thus not adequately resolved in the model, and are beyond the scope of the paper, which focuses on freshwater export across the shelf break.
To force the trajectory model, u- and v-wind fields at 10 m of elevation were taken from the National Centers for Environmental Prediction (NCEP) data, and applied with a fraction f of 3 and 7%, respectively (NCEP re-analysis data from the Physical Sciences Division, Earth System Research Laboratory, National Oceanic and Atmospheric Administration, are accessible from http://www.cdc.noaa.gov; see Kalnay et al.
1996). The value of 3% lies within the range of observations (2.3–3.2%) that have been reported previously (Rossby & Montgomery
1935; Haines & Bryson
1961). We also forced the model with 7% wind speeds, as tracer distributions from the Arctic suggest residence times for the surface layer that imply considerably higher transport velocities (Guay et al.
2001; Bauch et al.
2003; Bauch et al.
2005), possibly stimulated by the anomalously strong and pronounced pycnocline in the Arctic, which permits a fast-moving surface layer to “slide” over a decoupled subpycnocline layer, as proposed by Guay et al. (2001). Whenever a tracer crossed the land–sea boundary, the vector component perpendicular to the land–sea boundary is set to zero, and the component parallel with the boundary is reduced by 90% to account for energy loss as a result of increased turbulence. With this configuration the model predicts trajectories and end positions of individual Lagrangian particles for a given date. In our experiments particles (91 in total) were deployed daily at a position in the vicinity of the Lena River mouth (73.5°N, 130.5°E) from 1 June to 30 August, corresponding to the Lena River main discharge period. The tracer distribution is investigated for 16 September, which falls in the usual time frame for summer expeditions and data collection. Sensitivity to altered start positions (in a radius of 90 km) was tested in seven ensemble runs, and no substantial differences among the ensemble members were found in the tracer distribution. A trajectory index is defined using the results of all seven ensemble members. The index is the normalized mean distance between the end and start position of the tracer (scaled to the maximum value of the runs with an application of 3% wind forcing). Years were classified into “onshore” years and “offshore” years according to whether the majority of Lagrangian particles were transported to the south (onshore) or to the north (offshore). For the index, particles moved to the south were neglected in offshore years and particles moved to the north were neglected in onshore years because the asymmetric land–sea distribution substantially limits the travelling path for onshore particles as a result of the land boundary. As a consequence, just a few particles (representing only a small number of the total particles) moving far offshore during onshore years may be sufficient to turn the index unrealistically from on- to offshore.
Results
Hydrography and δ18O / salinity at the Laptev Sea continental margin
The vast Siberian Shelf regions cover more than onethird of the total Arctic Ocean area, and receive freshwater from several large rivers, with 394 km3 yr−1 from the Ob River (RosHydromet gauge data at Salekhard, from 1930 to 1999) and 580 km3 yr−1 from the Yenisey River (RosHydromet gauge data at Igarka, from 1936 to 1999) in the Kara Sea, and about 541 km3 yr−1 from the Lena River (RosHydromet gauge data at Kusur, from 1985 to 2007) in the Laptev Sea (Fig. 1). (RosHydromet gauge data are accessible at http://www.r-Arcticnet.sr.unh.edu through the Regional, Eletronic Hydrographic Data Network for the Arctic Region.) Maximal discharge of Arctic rivers occurs in the summer, and for the Lena River the main outflow during June and July is about four or five times higher than the annual mean discharge. The shelf regions are free of sea ice during summer and meltwater is released during this period, whereas sea-ice and brine waters are formed during winter. Because of the strong seasonal variability in river runoff and sea-ice cover, the hydrographic features of the Laptev Sea Shelf are subject to strong seasonal changes. The vertical stratification of the water column is most pronounced during summer, when the Lena River discharge is enhanced, sea ice is melting and the surface temperatures are highest because of both the relatively warm river water and exposure to high solar radiation (Bauch, Dmitrenko, Kirillov et al.
2009). Along the continental margin of the Eurasian Basin, surface waters are generally transported in an eastward direction (e.g., Newton et al.
2008). River water found at the continental margin of the Laptev Sea may therefore originate from the Ob and Yenisey rivers located to the south-east of the study area in the Kara Sea, as well as from the Lena River located to the south in the Laptev Sea. As a result of alongshore eastward transport, Lena River water may also be transported to the Eurasian Basin via the East Siberian Sea. Below about 300 m water depth the main core of the Atlantic Layer is moving along the continental slope in the eastward direction (e.g., Polyakov & Timokhov
1994).
River water in the Arctic is highly depleted in its stable oxygen δ18O isotope composition relative to marine water (see, e.g., the summary in Ekwurzel et al.
2001). Accordingly the δ18O results at the Laptev Sea Shelf break (Fig. 2) are dominated by a mixture of Lena River water with about −19‰ in δ18O (Mueller-Lupp et al.
2003) and marine water with a δ18O close to 0‰ (compare solid mixing line in (Fig. 2). Any deviations from this direct mixing between river water and marine water can be attributed to sea-ice processes: sea-ice formation adds brine to the water column and its salinity increases concurrent with nearly constant (slightly decreased) δ18O values, whereas the melting of sea ice adds freshwater, and the salinity of the water decreases at a nearly constant δ18O signature (slightly increased).
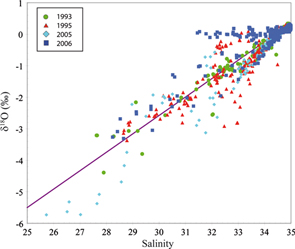
Fig. 2
Property plot of δ18O versus salinity for stations taken in 1993, 1995, 2005 and 2006. A mixing line between values of Atlantic water and Lena River water is indicated.
River water and sea-ice meltwater inventories based on δ18O and salinity data
The river water and sea-ice meltwater contributions can be quantified by applying a mass-balance calculation (e.g., Bauch et al.
1995). It is assumed that each sample is a mixture between marine water (f
mar), river runoff (f
r) and sea-ice meltwater (f
i). The balance is governed by the following equations:
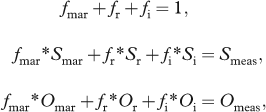
where f
mar, f
r and f
i are the fractions of marine water, river runoff and sea-ice meltwater in a water parcel, and S
mar, S
r, S
i, O
mar, O
r and O
i are the corresponding salinities and δ18O values. S
meas and O
meas are the measured salinity and δ18O of the water samples. The influence of Pacific waters entering the Arctic Ocean via the Bering Strait is generally negligible within the Eurasian Basin of the Arctic Ocean (Bauch et al.
1995; Ekwurzel et al.
2001), but was found to penetrate up to about 155°E at the continental margin of the East Siberian Sea in 2007 (Abrahamsen et al.
2009).
A special selection of salinity and d18O end-member values (Table 1) is required for each individual region (Bauch et al.
2003). The marine source is chosen according to the Atlantic Layer in the southern Nansen Basin (34.92 salinity and 0.3‰ in δ18O; Bauch et al.
1995). A mean value of river runoff within the Arctic Ocean of −20‰ (Bauch et al.
1995; Frank
1996) is taken as the river water end member. The choice of −20‰ instead of the slightly higher Lena River δ18O values (−19‰) prevents an overestimation of the river water (f
r) and brine components (negative f
i) at the shelf break, and gives proportionally altered values on the Laptev Sea Shelf. At the Laptev Sea Shelf break, differences are generally smaller than 1% in both fractions. For sea-ice meltwater the δ18O value of surface water at each station together with a fractionation of 2.6‰ (Melling & Moore
1995) is taken, and a salinity of 4 as measured for multiyear ice is assumed (Pfirman et al.
2004). A negative sea-ice meltwater fraction reflects the volume of water removed by sea-ice formation and the subsequent addition of brines to the remaining water column.
Table 1. End-member values for mass-balance calculations.
| End-member |
Salinity |
δ18O (‰) |
| Marine |
34.92 |
0.3 |
| River (f
r) |
0 |
−20 |
| Sea ice (f
i) |
4 |
surface +2.6‰ |
|
Inventory values of river water and sea-ice meltwater can be derived when integrating the calculated fractions over the depth of the water column. This is performed for all stations down to a constant water depth of 300 m (or bottom depth), which is approximately the depth of the Atlantic Layer. As most of the river water is found within the upper 100 m water depth, the choice of the integration depth is not critical to relative values, but rather adds a systematic offset, which is generally below 10% of the total inventory value. River water and sea-ice meltwater inventory values (Fig. 3) represent the thickness of the water column containing pure river water or sea-ice meltwater, respectively. Negative inventory values for sea-ice meltwater represent the thickness of the water column removed by sea-ice formation. All fractions and inventory values are net values reconstructed from the δ18O and salinity signature of each sample, and are the result of time-integrated effects on the sample volume.
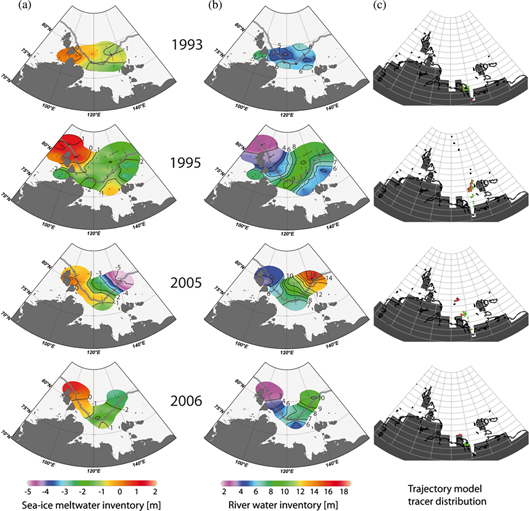
Fig. 3
Inventories of (a) sea-ice meltwater and (b) river water for all investigated years. The grey line indicates the 500-m isobath and the position of the continental slope. (c) Final distribution of Lagrangian particles derived from National Centers for Environmental Prediction wind data by applying a simple tracer trajectory numerical model, with particles released daily during June (black dots), July (red dots) and August (green dots), and with the final distribution depicted on 16 September. See text for further explanation.
To the north-west of the Laptev Sea, river water inventory values are consistently between 3 and 5 m, and increase towards the east, where absolute values are quite variable (Fig. 3). In 1993 and 2006, values of river water inventories above 8 m are absent, or are only found east of about 138°E, whereas in 1995 and 2005, river water values above 8 m are also found further to the west, at 125°E and 134°E, respectively. This suggests that the transport of river water in 1995 and 2005 may also occur directly to the north, whereas in 1993 and 2006 the river water left the Laptev Sea further to the east, or was possibly a remnant from preceding years only. In 1995 relatively high river water inventory values were observed over a rather large area, whereas in 2005 extremely high values, up to 18 m in the river water inventory, were found in a comparably small area. Sea-ice meltwater inventory values are positive north-west of the Laptev Sea, and are increasingly negative towards the east.
Trajectory approach to simulate the spread of river Lagrangian particles
A simple numerical model is used to time-integrate the effects of the daily mean atmospheric fields and calculate tracer trajectories, as described within the methods section. In our experiments Lagrangian particles (91 in total) were deployed daily at a position in the vicinity of the Lena River mouth (73.5°N, 130.5°E), starting on 1 June, when about 80% of the Laptev Sea is still ice covered, until 30 August, when the Laptev Sea is generally free of ice. The model applies a wind forcing during times when part of the area is still covered in sea ice, and therefore the model probably overestimates the drift path. The model clearly distinguishes between “onshore” (1993 and 2006) and “offshore” (1995 and 2005) atmospheric regimes over the Laptev Sea Shelf when comparing single years (Fig. 3c).
Comparison between the trajectory index, calculated from model results with 3% (Fig. 4) and 7% (Fig. 4) atmospheric wind forcing, and vorticity index (Fig. 4), shows a generally good and consistent correlation. For single years, such as 1999, our trajectory index and the vorticity index show contradicting results. The differences between applying 3% and 7% wind forcing are qualitatively insignificant: during onshore years they are virtually indistinguishable, whereas in offshore years the early deployed Lagrangian particles travel somewhat farther off shore. Owing to the small differences and because of qualitative and relative evaluations we will only discuss the 7% simulations for the following investigations.
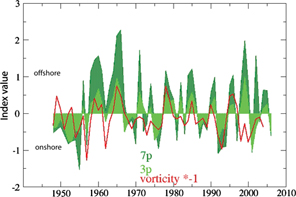
Fig. 4
Comparison between our normalized trajectory index calculated from model results with 3% (light green) and 7% (dark green) atmospheric wind forcing and the vorticity index (red line; inverted values). See text for further explanation.
Discussion
River inventories (I
riv) and sea-ice meltwater inventories (I
ice) show a common pattern for all of the years investigated (Fig. 3). The increase of I
riv within the Eurasian Basin from the west to the east along the Laptev Sea continental slope is in accordance with the addition of river water from the Lena River at the Laptev Sea continental margin. The concurrent decrease of I
ice from positive values in the north-west of the Laptev Sea to increasingly negative inventory values towards the north-east accords with the addition of brine waters, which have been shown to enter the Arctic Ocean halocline from the Laptev Sea, and are released from the shelf predominantly by wind forcing, similarly to river water (Bauch, Dmitrenko, Wegner et al.
2009). Positive sea-ice meltwater inventories in the north-west of the Laptev Sea indicate a net influence of sea-ice melting in this area during the summer season. In the north-east of the Laptev Sea continental margin, negative sea-ice meltwater inventory values indicate a predominant influence of sea-ice formation, even during the summer season when sea-ice also melts locally in this area. Directly north of the Laptev Sea at the continental slope, river water inventories are relatively low compared with values further east, which indicates that river water is leaving the Laptev Sea in the very east, along the northern coast of the New Siberian Islands, or via the adjacent East Siberian Sea.
The common pattern in river and sea-ice meltwater inventories is found in all years, despite the observed strong interannual variations. A correlation between river and sea-ice meltwater patterns was also observed at the continental slope of the Beaufort Shelf (Yamamoto-Kawai et al.
2008), but distribution patterns of river and sea-ice meltwater fractions in the surface layer have been found to show independent interannual variations and distribution patterns in recent years (Yamamoto-Kawai et al.
2008). The correlation of river and sea-ice meltwater inventories at the Laptev Sea continental slope suggests that source region and transport mechanisms are closely linked over the relatively shallow Laptev Sea Shelf, in agreement with the concept that both river water and sea-ice meltwater originate at the shallow south-eastern Laptev Sea Shelf, and are released by wind forcing (Bauch, Dmitrenko, Wegner et al.
2009).
As the atmospheric dynamics during summer are believed to control the freshwater release from the Laptev Sea (Guay et al.
2001; Johnson & Polyakov
2001; Dmitrenko et al.
2005; Dmitrenko et al.
2008), we will try to explain the observed interannual variations in freshwater inventories as a response to atmospheric circulation. The vorticity index generally describes the largescale atmospheric circulation around the Laptev Sea, but deviates from hydrographic observations for some years. For example, in 1999 a positive vorticity index indicates onshore transport of river water in the Laptev Sea, whereas hydrographic observations indicate an offshore transport of low-salinity river water (Fig. 5c). To better describe years that do not seem to be properly described with the vorticity index (see below), and to also explain the observed interannual variations in the distribution of river water off the shelf break (see below), we apply a simple numerical Ekman drift trajectory model forced by wind data. For a consistency check, simple budget considerations for river water inventories are carried out and compared with annual Lena River discharge values (see below). To analyse our results in the context of long-term variability, the relationship of recurring local wind regimes over the Laptev Sea to large-scale atmospheric modes of the SLP field, such as the NAO/AO, is investigated (see below).
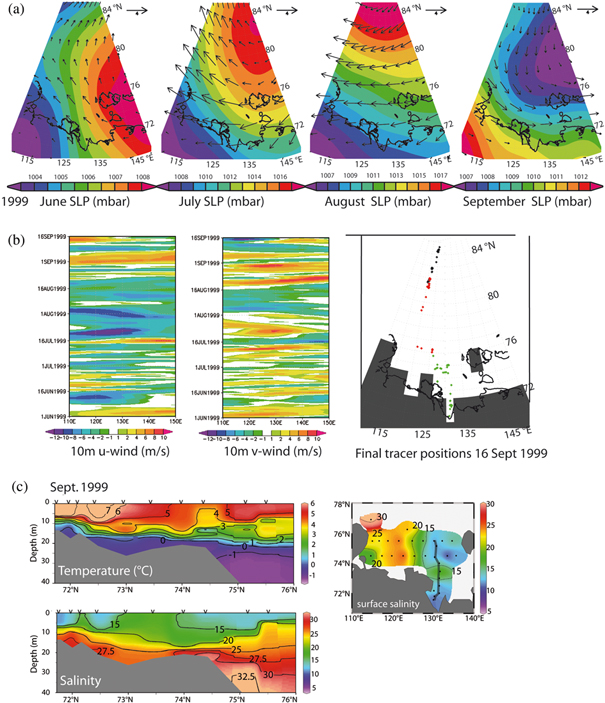
Fig. 5
(a) Series of monthly averaged National Centers for Environmental Prediction 10-m winds (given in m s−1) with an offshore wind setting in June and July, and with the opposite wind direction during September. The sea-level pressure from June to September 1999 is indicated by the coloured shading. Note the different scaling of the sea-level pressure (SLP) colour bar. (b) Variability of wind direction and velocity from a 10-m elevation in m s−1 during summer 1999. The left panel shows the zonal wind component at 75°N (10-m u-wind) and the middle panel shows the meridional wind component at 75°N (10-m v-wind), where positive values indicate eastward and northward directions, respectively. The right panel shows the final positions of Lagrangian particles deployed in June (black dots), July (red dots) and August (green dots) on 16 September 1999. See text for further explanation. (c) Temperature and salinity data on an oceanographic section roughly along 130°E latitude as well as the surface salinity distribution in September 1999.
Description of the atmospheric conditions and its reflection in river water distribution in 1999
A simple way to classify the summer atmospheric pattern is by visual inspection, for example, of the monthly averaged geostrophic winds during the summer months, following the method described by Guay et al. (2001); see the 1999 data in Fig. 5a for an example. Dmitrenko et al. (2005) use the vorticity index defined by Walsh et al. (1996), which generalizes SLP for an area within a radius of 550 km of 85°N and 125°E, a region located in the Arctic Ocean to the north of the Laptev Sea, and is calculated as the numerator of the finite-difference Laplacian of SLP data from June to September. Years with predominantly northerly and westerly winds over the Laptev Sea during June to September tend to cause an onshore or along-shore surface water transport, and are characterized as “onshore” years (Guay et al.
2001). These years mostly have a positive vorticity index, which corresponds to a large-scale cyclonic atmospheric circulation. Years with predominantly southerly to southeasterly winds, in contrast, tend to cause an offshore transport of surface waters, and are characterized as “offshore” years (Guay et al.
2001); they generally have a negative vorticity index, which corresponds to a large-scale anticyclonic atmospheric circulation. When evaluating wind data visually, for example, looking at the monthly mean wind data (see 1999 data in Fig. 5a), short-term deviating events are smoothed out and single deviating months are merely excluded. For example, in June and July 1999 data indicate “offshore”, whereas September data indicate “onshore” (Fig. 5a). The vorticity index is defined over a relatively large area, and by reducing a two-dimensional field to a one-dimensional index it loses information, i.e., spatial variance. Besides these drawbacks both methods do not consider the more complex interaction at the air–sea interface.
The trajectory index is based on the same original wind data, but indicates, contrary to the vorticity index, a clear and significant offshore transport of river water, and gives a clear “offshore” classification of this year (Fig. 4, 5b). Observations from 1999 in the Laptev Sea (Fig. 5c) show relatively low salinities in the northern Laptev Sea compared with long-term mean values, and thereby indicate an offshore transport of river water in 1999, justifying the trajectory approach. Whereas in most years the averaging of atmospheric conditions over the entire region and time period (vorticity index, monthly wind fields) and the model results (trajectory index) leads to rather similar results, significant differences are observed in years with strong temporally and spatially variable wind settings, such as those of 1999. Visual inspection of the final positions in 1999 shows that Lagrangian particles deployed between 1 June and 23 July (Fig. 5b), when discharge rates of the Lena River are highest, moved farthest to the north. Particles deployed after 23 July and after mid-August showed only a moderate northward drift (Fig. 5b), and some moved to the south (Fig. 5b), during a time when the Lena River discharge had already strongly declined. Comparison with observations (Fig. 5c) shows that the trajectory approach characterizes the offshore setting of this year correctly. The fact that the trajectory index shows better results is in agreement with studies that demonstrate that the on/offshore movement of river water plumes is strongly controlled by local winds (e.g., Yankovsky
2000; Chapman & Lentz
2005), which are only loosely connected to larger scale circulation patterns, as expressed by the vorticity index.
Interannual variations in inventory values
Observed distributions in river inventories show strong interannual variations similar to the final distributions of river water trajectories, which show two clearly different regimes: in “onshore” years (1993 and 2006 in Fig. 3) Lagrangian particles are found close to the Lena River mouth and near the coast; in “offshore” years (1995 and 2005 in Fig. 3) they are found mostly at or beyond the position of the Laptev Sea continental slope. The observed distributions in river inventories show similar variations: in 1993 and 2006 river water inventories are relatively low, and values above 8 m are found only east of about 138°E, whereas values of similar magnitude are also found further to the west at 125°E and 134°E in 1995 and 2005, respectively. These distributions suggest that river water is exported at the Laptev Sea Shelf break primarily during offshore years, whereas during onshore years export is strongly reduced or is not directly transported to the north.
Even between the two “offshore” years 1995 and 2005 there are considerable differences in the observed river inventories. In the 2005 “offshore” year, the peak values of river inventories are distinctively higher compared with those of 1995. Discharge values of the Lena River in 2005 (550 km3) are somewhat higher compared with 488 km3 in 1995, but cannot account for the observed differences in river inventories. We use the trajectory approach to obtain evidence for the atmospheric influence on the river water distribution for the two offshore years by evaluating the relative distributions of Lagrangian particles: In 1995 the final distribution of particles is stretched over a large latitudinal distance, and the particles released during June extend much further to the north (Fig. 3). In 2005, river particles released until 11 July were all found within a small region, separated by amean distance of only 127 km (see Fig. 3 at about 77°N). These particles represent 55% (196 km3) of the discharge released during June–August 2005 (354 km3). In 1995, when particles were deployed from 1 June to 3 July, the mean distance between particles was 228 km (Fig. 3), which represents nearly the same absolute and relative level of discharge (55% and 196 km3). This suggests that in 1995 near-surface winds distributed the main river plume over a large area, whereas in 2005 they pushed the main river water plume without spreading and thinning it. To support this hypothesis, we carry out some semiquantitative river water budget calculations integrated over appropriately selected areas with idealized geometry for these two years.
Budget considerations for river inventory values
A budget of river water is calculated for the area where maximal inventory values have been observed in the investigated years. The choice of this area is limited by the station coverage, and at the same time determines crucially the absolute values. Therefore this budget is a rough first-order estimate only. Our budget also ignores differences in residence times, and assumes a residence time of below one year for Laptev Sea river water in the upper water column. As there are indications that the residence time can be considerably longer than one year (e.g., Dmitrenko et al.
2008), our budget considerations are a test of this simplification during offshore years. For a comparison of river water budgets in 1995 and 2005, river water inventories of both years are at first integrated over a constant area reaching from 135°E to 150.15°E, and from 78.8°N to 81.2°N (about 78×103 km2). Average river water inventories I
riv within this area are 8.2 and 14.0 m in 1995 and 2005, respectively, and total river budgets of 634 and 1092 km3 are calculated for 1995 and 2005, respectively (Table 2). These budgets are much larger than the annual discharge values of the Lena River, which are 488 and 550 km3 for 1995 and 2005, respectively (RosHydromet gauge data at Kusur are accessible at http://www.r-Arcticnet.sr.unh.edu through the Regional, Eletronic Hydrographic Data Network for the Arctic Region). When we compare the calculated budgets (634 and 1092 km3) with the annual discharge values of the Lena River (488 and 550 km3), the imported contribution from the Kara Sea has to be subtracted. For this purpose the average height in the river inventory of the region near Severnaya Zemlya in the north-west of the Laptev Sea of 3–4 m (Table 2) is taken and subtracted from the average river inventory values. This approach assumes a steady eastward transport rate of river water from the Kara Sea along the shelf break without further mixing. The resulting river budgets for the Laptev Sea (Table 2) are within the range of the Lena River discharge values, and account for 77 and 140% of the discharge in 1995 and 2005, respectively, suggesting that the choice of the reference area is probably too narrow in 1995 and too wide in 2005. When we now approach a consistency consideration from the opposite perspective, and divide the annual Lena River discharge by the calculated average river inventory contribution from the Laptev Sea, we obtain an idealized distribution area of about 93×103 and 56×103 km2for 1995 and 2005, respectively. This estimate suggests that in 1995 the annual river water of the Lena River is spread over an area 1.7 times larger compared with 2005. As shown before, the relative stretching of Lagrangian particles derived in the trajectory model give a relation of 1.8 for the mean distances between river particles representing the main river plumes of the two years.
Table 2. Summary of river inventories and river budgets calculated for both years over the reference area between 135°E and 150.15°E, and 78.8°N and 81.2°N (77 822 km2). See text for further explanation.
| Year |
Average inventory heighta
|
Kara Sea inventory heightb
|
Total river budgeta
|
Laptev Sea river budgetc
|
Lena discharged
|
Calculated area of Lena River watere
|
| 1995 |
8.2 m |
3.4 m |
634 km3
|
374 km3
|
488 km3
|
93 333 km2
|
| 2005 |
14.0 m |
4.1 m |
1092 km3
|
772 km3
|
550 km3
|
55 556 km2
|
aThe average inventory height is based on all stations within the reference area and taken over the area to derive the total river budget.
|
bThe Kara Sea inventory height refers to the average river inventory height observed to the north-east of the Laptev Sea.
|
cThe Laptev Sea river budget is calculated over the reference area from the difference between average inventory height and Kara Sea inventory height.
|
dThe Lena discharge refers to the annual Lena River discharge.
|
eThe calculated area of Lena river water is determined as the ratio of Lena discharge and the difference between average inventory height and Kara Sea inventory height.
|
|
Both estimates are rough, but they are independently derived and show general consistency. Based on various simplifying assumptions the estimates suggest that during years with a predominant “offshore” wind regime the volume of river water released at the shelf break of the Laptev Sea could be on the same order of magnitude as the volume of river water released by the Lena River. This would mean that the residence time of river water in the Laptev Sea during years with predominant “offshore” winds may be as low as one year. By contrast, in years with predominant “onshore” wind regimes, the residence time of Lena River water on the shelf will be longer, and river water will eventually enter the Arctic Ocean halocline or surface layer in a consecutive year, and possibly via the East Siberian Sea. Further support for this hypothesis has been provided recently by Dmitrenko et al. (2008): their analysis of freshwater content anomalies of the Laptev and East Siberian seas shows that its variation is about 35% of the annual volume of river and local sea-ice meltwater, and that freshwater is redistributed between the Laptev Sea and the East Siberian Sea, as well as exported to the Arctic Ocean, in correlation with atmospheric circulation. This is in agreement with our results, which suggest that during years with predominantly “offshore” winds, freshwater is exported rapidly north of the Laptev Sea, and probably also from the East Siberian Sea. Of course, because of its simplified dynamics the Ekman drift trajectory model underestimates transports along the coast, as the piling up of water during onshore conditions would clearly stimulate strong horizontal pressure gradients, establishing an eastward coastal current. Moreover, as we are missing tracer data from the shelf break of the East Siberian Sea we can only speculate about the pathways and volumes of Lena River water entering the Arctic Ocean halocline via this passage.
Correlation with regional atmospheric dynamics
So far we have shown the existence of two different modes of atmospheric forcing, and its impact on the distribution of river water over the Laptev Sea Shelf. Both the vorticity and the trajectory monitoring tools strongly imply cyclic dynamics, with recurring on- and offshore periods. Summer salinity trends recorded on several Siberian Shelf seas indicate a close relationship to winter AO/NAO on decadal timescales (Steele et al. 2004). Surprisingly, we cannot see a clear relationship between various AO/NAO indices and the vorticity and trajectory indices (not shown). This indicates that the transport of river water, and its further distribution in the Laptev Sea, is governed by physical processes other (more local) than the AO/NAO, which instead controls the total freshwater supply into the Siberian drainage basins.
In order to identify the relevant mode of atmospheric variability, and to asses its spatial scale, we further analyse the summer SLP variability north of 50°N using empirical orthogonal functions (EOFs; Preisendorfer
1988). Note that the classical AO is defined as the first EOF of the SLP during winter (Thompson & Wallace
2000), when it is generally more pronounced than during summer months. By solving the eigenvalue problem for the covariance matrix this method finds spatial patterns of variability (EOFs) and their variation in time (principal components, PCs) by turning the coordinate axis in the direction of highest variance.
The leading EOF of the SLP during summer (not shown) describes the variability associated with the Polar High and the Iceland Low, and explains 37% of total SLP variance north of 50°N. The second and third EOF of the summer SLP (Fig. 6a, b) account for 12 and 10% of total SLP variance, respectively. In contrast to the leading EOF, the second and third EOFs exhibit a dipole pattern similar to the trajectory and the vorticity indices. The low seen in the third EOF over the northern Laptev Sea explains up to 42% of the total SLP variance in this area. And the derived PC from the third EOF exhibits good covariance with the trajectory and vorticity index (Fig. 7). Positive trajectory indices indicating offshore conditions are associated with negative expansion coefficients. Thus, the corresponding third EOF (Fig. 7b) would postulate an anomalous high SLP in the northern Laptev Sea during offshore years, and an anomalous low SLP during onshore years, when expansion coefficients of the PC of the third EOF are negative. To test this hypothesis we calculated SLP anomalies for years with trajectory indices higher than 0.5 (offshore years) and indices lower than 0.5 (onshore years). Consistent with the results of the EOF analysis, offshore years are marked by a pronounced positive SLP anomaly (Fig. 6d) over the northern Laptev Sea, and onshore years exhibit an anomalous low SLP (Fig. 6c).
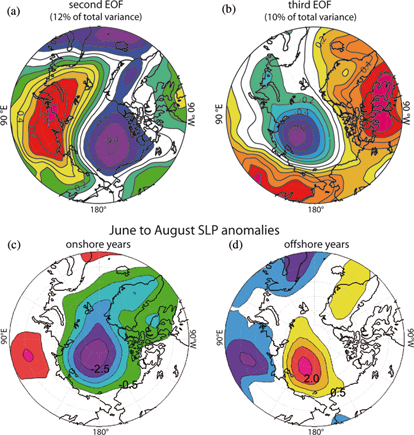
Fig. 6
Empirical orthogonal function (EOF) patterns for sea-level pressure (SLP) summer data presented as correlation maps between the expansion coefficient time series and SLP data for (a) the second EOF and (b) the third EOF. See text for further explanation. Average June–August SLP anomalies (difference to the climatological mean for summers from 1948 to 2007) during (c) onshore years and (d) offshore years.
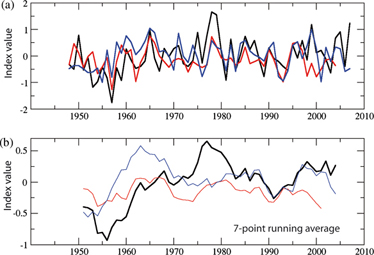
Fig. 7
(a) Comparison between the trajectory index (blue), the inverted vorticity index (red) and (b) the inverted principle component time series from the third empirical orthogonal function of summer sea-level pressure data (black) north of 50°N. (b) Seven-point running average for the curves displayed in (a).
This strongly implies that the third EOF pattern represents the relevant mode of variability, which determines local wind and SLP fields, and thus the distribution of river water on the Laptev Shelf, whereas the first and second EOFs are only of minor importance. These results show that the wind-induced transport of river water is related to local SLP patterns that contribute only about 10% to the total SLP variance north of 50°N during summer. The underlying physical pattern is controlled by the relative position of travelling local lows generated over the heated Siberian landmass during summer, and local highs in the north emerging over the Arctic Ocean (e.g., Maslanik et al.
1996; Wang et al.
2009).
Summary and conclusions
Considerable interannual differences are observed in river water inventory values, which are derived from δ18O and salinity values in the eastern Eurasian Basin, along the continental margin of the Laptev Sea. The annually different patterns in river and sea-ice meltwater inventories at the Laptev Sea continental slope remain closely linked for all years. This correlation between river and sea-ice meltwater inventories indicates that source regions and transport mechanisms for both river water and sea-ice formation are largely similar over the relatively shallow shelf.
An Ekman drift trajectory model driven by daily NCEP 10-m wind fields demonstrates that atmospheric conditions alone can force different transport paths of river water, and can explain the main differences between years with onshore or offshore wind patterns, as well as the observed interannual differences between river water distributions observed for years with rather similar offshore wind regimes. Comparison of river water budgets at the Laptev Sea continental margin with Lena River annual discharge rates are consistent with the assumption of a residence time for river water during “offshore” years being as short as just one year. Comparison of the vorticity index with the newly developed trajectory index shows, in general, a good correlation between the two indices. Contradicting results are obtained for years with a high temporal variability, and comparison with hydrographic data show that the trajectory index correctly describes the influence of the atmospheric circulation regime on the river water distribution in the Laptev Sea. The wind conditions in the Laptev Sea are related to local SLP patterns that contribute only roughly 10% to the total summer SLP variance north of 50°N. These local SLP patterns are built up by the relative pathway of travelling lows generated over the heated Siberian landmass during summer, and local highs in the north emerging over the Arctic Sea, and are decoupled from the AO/NAO.
Regarding a possible freshening of the Arctic (Peterson et al.
2002) and the future stability of the Arctic halocline, our results imply that it is not sufficient to look only at long-term trends in salinity records, which are more sensitive to the total volume of freshwater input from rivers (Steele et al. 2004). The distribution of this freshwater and its export into the Arctic Basin will determine and maintain the unique halocline structure of the Arctic. Our results indicate that this export is controlled by local atmospheric circulation patterns. These small-scale structures are, however, less predictable by global climate models, with their coarse spatial resolution. In these models the climate feedback given by the Arctic halocline is therefore probably not yet adequately resolved.
Acknowledgements
We thank all members of the NABOS project for exceptional working conditions and extensive support during expeditions. DB acknowledges funds from the German Research Foundation grant SP 526/3; MG acknowledges funds from the Federal Ministry of Education and Research grant 03G0639D; and ID acknowledges funds from the Federal Ministry of Education and Research grant 03G0639A. SK and ET acknowledge funding through the Federal Ministry of Education and Research project Otto-Schmidt-Laboratory for Polar and Marine Sciences (03PL038A). We would like to thank Robert Newton for his constructive review on the article, resulting in a significant improvement of the article. We thank an anonymous reviewer for valuable comments that also helped to improve the article.
References
Abrahamsen E.P., Meredith M.P., Falkner K.K., Torres-Valde S., Leng M.J., Alkire M.B., Bacon S., Laxon S., Polyakov I., Ivanov V. & Kirillov S. 2009. Tracer-derived freshwater composition of the Siberian continental shelf following the extreme Arctic summer of 2007. Geophysical Research Letters 36, L07602, doi: 10.1029/2009GL037341.
[Crossref].
Bauch D., Dmitrenko I.A., Kirillov S.A., Wegner C., Hölemann J., Pivovarov S., Timokhov L.A. & Kassens H. 2009.
Eurasian Arctic shelf hydrography: exchange and residence time of southern Laptev Sea waters.
Continental Shelf Research
29,
1815–1820.
[Crossref]
Bauch D., Dmitrenko I.A., Wegner C., Hölemann J., Kirillov S.A., Timokhov L.A. & Kassens H. 2009. Exchange of Laptev Sea and Arctic Ocean halocline waters in response to atmospheric forcing. Journal of Geophysical Research—Oceans 114, C05008, doi: 10.1029/2008JC005062.
[Crossref].
Bauch D., Erlenkeuser H. & Andersen, N. 2005.
Water mass processes on Arctic shelves as revealed from 18O of H2O.
Global and Planetary Change 48,
165–174.
[Crossref].
Bauch D., Erlenkeuser H., Stanovoy V., Simstich J. & Spielhagen R.F. 2003. Freshwater distribution and brine waters in the southern Kara Sea in summer 1999 as depicted by δ18O results. In R. Stein et al. (eds.), Siberian river run-off in the Kara Sea: characterization, quantification, variability and environmental significance. Proceedings in Marine Science
6. Pp. 73–90. Amsterdam: Elsevier.
Bauch D., Schlosser P. & Fairbanks R.F. 1995.
Freshwater balance and the sources of deep and bottom waters in the Arctic Ocean inferred from the distribution of H2
18O.
Progress in Oceanography
35,
53–80.
[Crossref].
Craig H. 1961.
Standard for reporting concentrations of deuterium and oxygen-18 in natural waters.
Science
133,
1833–1834.
[Crossref].
Chapman D.C. & Lentz S.J 2005.
Acceleration of a stratified current over a sloping bottom, driven by an alongshelf pressure gradient.
Journal of Physical Oceanography
35,
1305–1317.
[Crossref].
Dmitrenko I.A., Kirillov S.A., Eicken H. & Markova N. 2005. Wind-driven summer surface hydrography of the eastern Siberian Shelf. Geophysical Research Letters 32, L14613, doi: 14610.11029/12005GL023022.
[Crossref].
Dmitrenko I.A., Kirillov S.A. & Tremblay L.B. 2008. The long-term and interannual variability of summer fresh water storage over the eastern Siberian Shelf: implication for climatic change. Journal of Geophysical Research—Oceans 113, C03007, doi: 03010.01029/02007JC004304.
[Crossref].
Ekwurzel B., Schlosser P., Mortlock R. & Fairbanks R. 2001.
River runoff, sea ice meltwater, and Pacific water distribution and mean residence times in the Arctic Ocean.
Journal of Geophysical Research—Oceans
106,
9075–9092.
[Crossref].
Frank M. 1996. Spurenstoffuntersuchungen zur Zirkulation im Eurasischen Becken des Nordpolarmeeres. (Tracer investigations of the circulation in the Eurasian Basin of the Arctic Ocean.) PhD thesis, University of Heidelberg.
Gawarkiewicz G. & Plueddemann A.J. 1995.
Topographic control of thermocline frontal structure in the Barents Sea Polar Front on the south flank of Spitsbergen Bank.
Journal of Geophysical Research—Oceans
100,
4509–4524.
[Crossref].
Guay C.K., Falkner K.K., Muench R.D., Mensch M., Frank M. & Bayer R. 2001.
Wind-driven transport pathways for Eurasian Arctic river discharge.
Journal of Geophysical Research—Oceans
106,
11469–11480.
[Crossref].
Haines D.A. & &. Bryson R.A. 1961.
An empirical study of wind factor in Lake Mendota.
Limnology and Oceanography
6,
356–364.
[Crossref].
Johnson M.A. & Polyakov I. 2001.
The Laptev Sea as a source for recent Arctic Ocean salinity changes.
Geophysical Research Letters
28,
2017–2020.
[Crossref].
Kalnay E., Kanamitsu M., Collins W., Deaven D., Gandin L., Iredell M., Saha S., White G., Woollen J., Zhu Y., Chelliah M., Ebisuzaki W., Higgins W., Janowiak J., Mo K.C., Ropelewski C., Wang J., Leetmaa A., Reynolds R., Jenne R. & Joseph, D. 1996.
The NCEP/NCAR 40-Year Reanalysis Project.
Bulletin of the American Meteorological Society
77,
437–471.
[Crossref].
Mackensen A. 2001.
Oxygen and carbon stable isotope tracers of Weddell Sea water masses: new data and some paleoceanographic implications.
Deep-Sea Research Part I
48,
1401–1422.
[Crossref].
Maslanik J.A., Serreze M.C. & Barr R.G. 1996.
Recent decreases in Arctic summer ice cover and linkages to atmospheric circulation anomalies.
Geophysical Research Letters
23,
1677–1680.
[Crossref].
Melling H. & Moore R. 1995.
Modification of halocline source waters during freezing on the Beaufort Sea Shelf: evidence from oxygen isotopes and dissolved nutrients.
Continental Shelf Research
15,
89–113.
[Crossref].
Mueller-Lupp T., Erlenkeuser H. & Bauch H.A. 2003.
Seasonal and interannual variability of Siberian river discharge in the Laptev Sea inferred from stable isotopes in modern bivalves.
Boreas
32,
292–303.
[Crossref].
Newton R., Schlosser P., Martinson D.G. & Maslowski W. 2008. Freshwater distribution in the Arctic Ocean: simulation with a high-resolution model and model-data comparison. Journal of Geophysical Research—Oceans 113, C05024, doi: 19410.11029/12004GL020666
[Crossref].
Peterson B.J., Holmes R.M., McLelleand J.W., Vörösmaty C.J., Lammers R.B., Shiklomanov A.I. & Rahmstorf S. 2002.
Increasing river discharge to the Arctic Ocean.
Science
298,
2171–2173.
[Crossref].
Pfirman S., Haxby W., Eicken H., Jeffries M. & Bauch D. 2004. Drifting Arctic sea ice archives changes in ocean surface conditions. Geophysical Research Letters 31, L19401, doi: 19410.11029/12004GL020666
[Crossref].
Polyakov I.V. & Timokhov L.A. 1994.
Mean fields of temperature and salinity of the Arctic Ocean.
Russian Meteorology and Hydrology
7,
33–38.
Preisendorfer R.W. 1988.
Principal component analysis in meteorology and oceanography.
New York: Elsevier.
Proshutinsky A.Y. & Johnson M.A. 1997.
Two circulation regimes of the wind-driven Arctic Ocean.
Journal of Geophysical Research—Oceans
102,
12493–12514.
[Crossref].
Rossby C.-G. & Montgomery R.B. 1935.
The layer of frictional influence in wind and ocean currents. Papers in Physical Oceanography and Meteorology 3(3).
Cambridge, MA: Massachusetts Institute of Technology and Woods Hole Oceanographic Institution.
[Crossref].
Schmidt G.A., Bigg G.R. & Rohling E.J. 1999. Global Seawater Oxygen-18 Database. Goddard Institute for Space Studies, National Aeronautics and Space Administration. Accessed on the internet at http://data.giss.nasa.gov/o18data in February 2008.
Steele M. & Ermold W. 2004. Salinity trends on the Siberian shelves. Geophysical Research Letters 31, L24308, doi: 10.1029/2004GL021302.
[Crossref].
Thompson D.W.J. & Wallace J.M. 2000.
Annular modes in the extratropical circulation. Part I: Month-to-month variability.
Journal of Climate
13,
1000–1016.
[Crossref].
Walsh J.E. Chapman W.L. & Shy T.L. 1996.
Recent decrease of sea level pressure in the central Arctic.
Journal of Climate
9,
480–486.
[Crossref].
Wang J., Zhang J., Watanabe E., Ikeda M., Mizobata K., Walsh J.E., Bai X. & Wu B. 2009. Is the Dipole Anomaly a major driver to record lows in Arctic summer sea ice extent? Geophysical Research Letters 36, L05706, doi: 05710.01029/02008GL036706.
[Crossref].
Yamamoto-Kawai M., McLaughlin F.A., Carmack E.C., Nishino S. & Shimada K. 2008. Freshwater budget of the Canada Basin, Arctic Ocean, from salinity, δ18O, and nutrients. Journal of Geophysical Research—Oceans 113, C01007, doi: 10.1029/2006JC003858
[Crossref].
Yankovsky A.E. 2000.
The cyclonic turning and propagation of buoyant coastal discharge along the shelf.
Journal of Marine Research
58,
585–607.
[Crossref].
Yankovsky A.E. & Chapman, D.C. 1997.
Anticyclonic eddies trapped on the continental shelf by topographic irregularities.
Journal of Geophysical Research—Oceans
102,
5625–5639.
[Crossref].