RESEARCH/REVIEW ARTICLE
Quantifying polynya ice production in the Laptev Sea with the COSMO model
Martin Bauer,1 David Schröder,2 Günther Heinemann,1 Sascha Willmes1 & Lars Ebner1
1 Environmental Meteorology, University of Trier, Behringstr. 21, DE-54296 Trier, Germany
2 Department of Meteorology, University of Reading, P.O. Box 243, RG6 6BB Reading, UK
Abstract
Arctic flaw polynyas are considered to be highly productive areas for the formation of sea-ice throughout the winter season. Most estimates of sea-ice production are based on the surface energy balance equation and use global re-analyses as atmospheric forcing, which are too coarse to take into account the impact of polynyas on the atmosphere. Additional errors in the estimates of polynya ice production may result from the methods of calculating atmospheric energy fluxes and the assumption of a thin-ice distribution within polynyas. The present study uses simulations using the mesoscale weather prediction model of the Consortium for Small-scale Modelling (COSMO), where polynya area is prescribed from satellite data. The polynya area is either assumed to be ice-free or to be covered with thin ice of 10 cm. Simulations have been performed for two winter periods (2007/08 and 2008/09). When using a realistic thin-ice thickness of 10 cm, sea-ice production in Laptev polynyas amount to 30 km3 and 73 km3 for the winters 2007/08 and 2008/09, respectively. The higher turbulent energy fluxes of open-water polynyas result in a 50–70% increase in sea-ice production (49 km3 in 2007/08 and 123 km3 in 2008/09). Our results suggest that previous studies have overestimated ice production in the Laptev Sea.
Keywords
Mesoscale modelling; Laptev Sea; polynya; ice production.
Correspondence
Martin Bauer, Environmental Meteorology, University of Trier, Behringstr. 21, DE-54296 Trier, Germany. E-mail: bauerm@uni-trier.de
(Published: 17 October 2013)
Polar Research 2013. © 2013 M. Bauer et al. This is an open-access article distributed under the terms of the Creative Commons Attribution-Noncommercial 3.0 Unported License (http://creativecommons.org/licenses/by-nc/3.0/), permitting all non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Citation: Polar Research 2013, 32, 20922, http://dx.doi.org/10.3402/polar.v32i0.20922
Polynyas are considered to cover 2–4% of the Arctic Ocean (Stringer & Groves 1991). These reoccurring open-water or thin-ice areas are of great importance in terms of ocean–atmosphere interactions (e.g., Smith et al. 1990; Barber & Massom 2007). Most Arctic polynyas are flaw polynyas, which are opened by off-shore winds and which often separate fast ice from drifting ice (Dethleff et al. 1998). The ice production rate in polynyas exceeds that over consolidated ice by, on average, one order of magnitude or more (e.g., Barber & Massom 2007).
As a region with frequent polynya openings, the Laptev Sea is considered one of the key areas for Arctic ice production. Past studies using different methods (e.g., Martin & Cavalieri 1989; Rigor & Colony 1997; Dethleff et al. 1998; Winsor & Björk 2000; Dmitrenko et al. 2009; Tamura & Ohshima 2011; Willmes et al. 2011; Rabenstein et al. 2013) have led to a large range of values for ice production for Laptev Sea polynyas.
Recent satellite-based studies by Martin et al. (2004), Willmes et al. (2011) and Tamura & Ohshima (2011) examined Arctic polynya ice production for different areas and time periods using passive microwave data in combination with coarse-resolution atmospheric data. Thin-ice thickness distribution in polynyas is either used as climatology or derived from the microwave data. Atmospheric data is taken from atmospheric reanalyses, which do not account for the feedback of polynyas with the atmospheric boundary layer. This may result in errors in the calculation of surface energy fluxes, which strongly determine ice production. In addition, the components of the net radiation are computed from near-surface reanalysis data by simple empirical formulae. Although all three studies mentioned above use the same satellite data—Special Sensor Microwave Imager (SSM/I)—the results differ greatly. Tamura & Ohshima (2011) calculate an ice production of 152 km3 per year for the Laptev Sea polynyas for the period September–May. When excluding the freeze-up months (September and October) and May, their study yields approximately 100 km3. This ice production is about twice as much as that estimated by Willmes et al. (2011): 55 km3 for the Laptev Sea polynyas in November–April. For the Chukchi Sea, the estimation by Martin et al. (2004) is also exceeded by the calculation of Tamura & Ohshima (2011) by a factor of two. This underlines the necessity of using additional independent methods for the estimation of ice production.
The presence of polynyas modifies the atmospheric boundary layer, resulting in a feedback on the surface energy fluxes, which is not considered in the above-mentioned satellite-based studies. Ebner et al. (2011) examined the influence of polynyas on the atmospheric boundary layer for idealized case studies using the mesoscale weather prediction model of the Consortium for Small-scale Modelling (COSMO; Steppeler et al. 2003). They concluded that the polynyas have a considerable impact by increasing the 2-m temperature (T2m) above open-water polynyas up to 10 K and increasing the wind speed up to 5 m s−1 (compared to identical simulations without polynyas). While higher T2m values may be considered to reduce the surface-layer instability (leading to decreased ice production), the higher wind speeds lead to increased ice production by enhanced heat export away from the polynya. Schröder et al. (2011) implemented a thermodynamic sea-ice model into COSMO and computed ice production rates for the Laptev polynyas for two weeks in April 2008. Their study demonstrated that high-resolution COSMO simulations yield realistic atmospheric conditions and can be used to examine ice production rates in polynyas.
The present study uses the same model set-up as Schröder et al. (2011) and applies it to the two complete winter periods of 2007/08 and 2008/09. Since one goal is to examine the influence of thin ice on ice production, simulations were performed using two different scenarios. The first assumes that the polynya is not covered by ice at all and the second assumes a uniformly distributed layer of thin—10 cm—ice on the polynya. The open-water scenario can be regarded as the maximum (potential) ice production, while the thin-ice scenario is considered to be more realistic since 10 cm corresponds approximately to the average thickness of ice on the Laptev polynyas derived by Willmes et al. (2011) using Moderate-resolution Imaging Spectroradiometer (MODIS) data. The winters 2007/08 and 2008/09 were chosen because of the availability of atmospheric and sea-ice data from winter field experiments (Heinemann et al. 2010). In addition, these two winters were associated with large differences in ice production. The winter 2008/09 showed a relatively large ice production, while 2007/08 was below average with respect to ice production.
Data and methods
Polynya area
Polynya area is derived from daily sea-ice concentration maps based on brightness temperatures of the Advanced Microwave Scanning Radiometer–Earth Observing System (AMSR-E; Spreen et al. 2008). AMSR-E sea-ice data have a resolution of 6.25 km, which is superior to SSM/I (12.5–25 km). All pixels with ice concentrations falling below a threshold of 70% (Massom et al. 1998) are treated as polynyas and subsequently an ice thickness of 0 or 10 cm is prescribed to COSMO for those areas. Adams et al. (2011) show that the 70% threshold yields polynya areas that agree well with those obtained by the polynya signature simulation method (Markus & Burns 1995). The ice thickness for sea-ice areas with ice concentrations exceeding 70% is set to 1 m. This value is in accordance with, for example, the value of 0.95 m used for the polar Weather Research and Forecasting model for ice concentration larger than 90% (Bromwich et al. 2001, 2005). Measurements of ice thickness in the Laptev Sea area by Rabenstein et al. (2013) show that ice is typically between 1.0 and 1.5 m thick in the vicinity of the polynya.
Model data
Atmospheric surface energy fluxes are the key variables when assessing polynya ice production. In our study, all fluxes were calculated by means of mesoscale model simulations. The non-hydrostatic, limited-area COSMO model was used. COSMO is the operational weather prediction model of the German Meteorological Service (Schättler et al. 2012). In addition to the operational application, the COSMO model provides a modelling framework for many scientific purposes, ranging from short case studies to climate simulations (e.g., Schröder et al. 2011; Gutjahr & Heinemann 2013). Turbulent fluxes at the surface are calculated using the Louis scheme (Louis 1979). Radiation fluxes are calculated according to Ritter & Geleyn (1992). A full description of the physical parameterizations is given by Doms et al. (2011).
Version 4.11 of the model was implemented with a horizontal resolution of 5 km for the Laptev Sea region (Fig. 1) by means of a two-step nesting. The initial data for the 15 km resolution domain was generated by interpolating from the German Meteorological Service’s global model (Majewski et al. 2002) with 40 km horizontal resolution to the 15 km grid. Boundary atmospheric conditions were provided by GME every 6 h. In the second nesting step the initial and boundary data needed for 5 km model resolution were taken from 15 km model runs every hour. The thermodynamic sea-ice model of Schröder et al. (2011) was used to simulate the sea-ice surface temperature (Ts) and energy fluxes over ice surfaces.
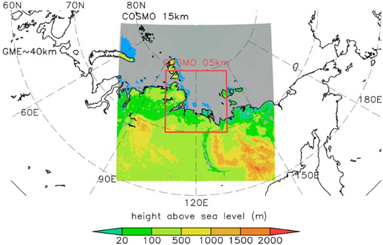
Fig. 1
Model domains of the weather prediction model of the Consortium for Small-scale Modelling (COSMO) 15 km and COSMO 5 km covering the Laptev Sea. The underlying map shows altitude over land. Polynya areas for 10 January 2009 are shown as blue areas. The German Meteorological Service’s global model (GME 40 km) provides forcing data for the COSMO 15 km model runs.
For comparison, we also used meteorological reanalysis data of the US National Centers for Environmental Prediction reanalysis data set (NCEP; Kanamitsu et al. 2002). NCEP data were chosen for a comparison with COSMO since many remote-sensing and sea-ice modelling studies use NCEP for forcing (e.g., Ernsdorf et al. 2011; Adams et al. 2013).
Assessment of ice production
As mentioned in the introduction, polynya area was either assumed to be ice-free (COSMO 0 cm, or C00) or to be covered with 10 cm of ice (COSMO 10 cm, or C10). To assess seasonal ice production, all model runs were conducted in a forecast mode for 30 h; the first 6 h were omitted as a spin-up period. The merging of the remaining 24-h periods generates continuous atmospheric data sets for the winters 2007/08 and 2008/09 (November–April). While conventional satellite-based methods (Yu & Lindsay 2003; Tamura & Ohshima 2011; Willmes et al. 2011) apply simple empirical formulas to calculate atmospheric energy fluxes, COSMO includes state-of-the-art parameterizations for turbulent fluxes and a radiation transfer scheme. In addition, our COSMO simulations took into account the effect of the polynya on the atmospheric boundary layer. In all methods, the calculation of ice production was based on the energy balance equation. If the water is at the freezing point, it is assumed that the total energy loss of the polynya surface to the atmosphere is compensated by freezing (oceanic heat flux is neglected), and the potential ice production can be described by the following equation:
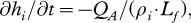
where QA is the total atmospheric heat flux, hi the ice thickness, ρi the density of sea ice (ρ=910 kg/m3) and the latent heat of freezing (Lf=0.334·106 J/kg). QA is calculated as
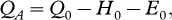
where Q0 is the net radiation balance, H0 is the sensible heat flux and E0 is the latent heat flux. Ice production will occur if the energy flux to the atmosphere QA is negative and the water is at its freezing point. The latter is generally observed throughout the winter period. Thin ice was kept constant during the model run, i.e., all newly formed ice was assumed to be transported away by advection, which is a realistic assumption for wind-driven flaw polynyas.
COSMO results are compared to Willmes et al. (2011), who used NCEP atmospheric data and the polynya signature simulation method for polynya area. Furthermore, the impact of polynyas on the atmospheric boundary layer is investigated by comparing NCEP-T2m and COSMO-T2m over polynyas and the entire Laptev Sea, respectively.
Results
Verification of COSMO
Verifying COSMO simulations in the vicinity of the Laptev polynyas is difficult due to the lack of observations. However, data are available from field measurements at the fast-ice edge in the Laptev Sea (Heinemann et al. 2010; Helbig et al. 2010) obtained from automatic weather stations as part of the German–Russian Laptev Sea System project during the Transdrift XIII/XV expeditions in April 2008 and April 2009. Mean biases and root mean square error (RMSE) between COSMO model variables and measurements of six automatic weather stations are −0.54 (1.54) m s−1 for wind speed, −0.72 (1.46) hPa for surface pressure, −1.02 (30.5) W m−2 for net radiation and −0.18 (2.74) K for T2m. This indicates a good quality of the simulations (see also Ernsdorf et al. 2011). Furthermore, Schröder et al. (2011) compared MODIS and COSMO surface temperatures and found that the sea-ice model implemented in COSMO performed well.
Time series of polynya parameters
Time series of polynya area, ice production and COSMO-T2m and NCEP-T2m are shown in Figs. 2 and 3. It should first be noted that there are large differences for polynya area and the volume of ice produced between the two winters (see Table 1). Daily and seasonal ice production within the Laptev Sea polynyas are highly variable, with daily values reaching up to 3 km3 d−1 and almost 6 km3 d−1 on 10 January 2009 for C10 and C00, respectively (Fig. 3d). Monthly values range from 0.4 to 27 km3 for C10. The longest period without polynyas is 21 days (3–24 March 2009). While typical polynya events lasted for about six days, the longest event—30 consecutive polynya days—spanned December 2008 and January 2009.
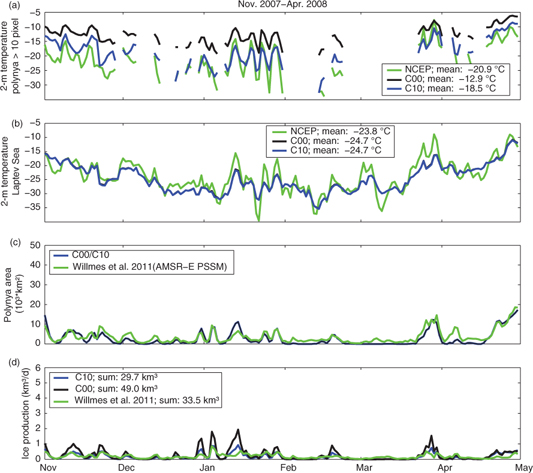
Fig. 2
Mean daily 2-m temperature for (a) polynyas and (b) the whole Laptev Sea, (c) polynya area and (d) sea-ice production in Laptev Sea polynyas in the winter of 2007/08. The model was that of the Consortium for Small-scale Modelling (COSMO), with a 5 km model domain. Time series are Willmes et al. (2011), COSMO with 10 cm of ice (C10) and COSMO with ice-free polynyas (C00). Missing values in (a) occur where polynya size is smaller than 300 km2 (corresponding to 10 model grid points). The figure abbreviates the following terms: National Centers for Environmental Prediction reanalysis data set (NCEP), Advanced Microwave Scanning Radiometer–Earth Observing System (AMSR-E) and the polynya signature simulation method (PSSM).
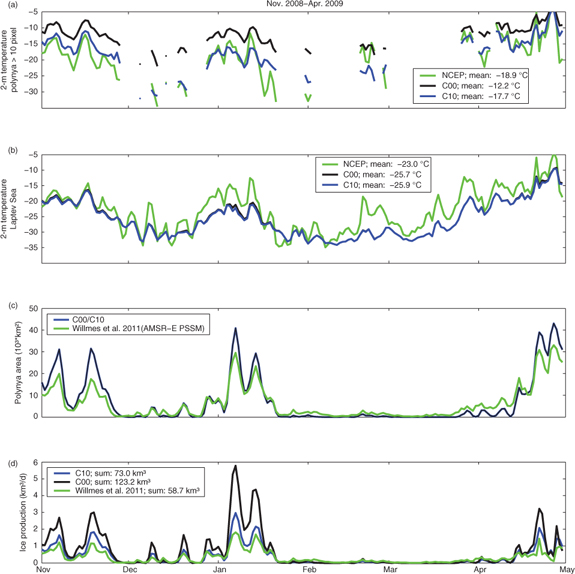
Fig. 3
Mean daily 2-m temperature for (a) polynyas and (b) the whole Laptev Sea, (c) polynya area and (d) sea-ice production in Laptev Sea polynyas in the winter of 2008/09. The model was that of the Consortium for Small-scale Modelling (COSMO), with a 5 km model domain. Time series are Willmes et al. (2011), COSMO with 10 cm of ice (C10) and COSMO with ice-free polynyas (C00). Missing values in (a) occur where polynya size is smaller than 300 km2 (corresponding to 10 model grid points). The figure abbreviates the following terms: National Centers for Environmental Prediction reanalysis data set (NCEP), Advanced Microwave Scanning Radiometer–Earth Observing System (AMSR-E) and the polynya signature simulation method (PSSM).
Table 1 Seasonal ice production sums (km3) for the model of the Consortium for Small-scale Modelling (COSMO) for ice-free (C00) conditions and 10 cm of sea-ice cover (C10) and the results of Willmes et al. (2011) for the entire Laptev Sea polynya area and the winters (November-April) of 2007/08 and 2008/09.
| |
2007/08 |
2008/09 |
| C10 |
30 |
73 |
| C00 |
49 |
123 |
| Willmes et al. |
34 |
59 |
Polynya openings are associated with temperature peaks and wind speed peaks (not shown), which can be expected for wind-driven flaw polynyas and which agrees well with the findings of Stringer & Groves (1991) for the Bering and Chukchi seas. Ice production values for COSMO runs with open-water polynyas exceed those with 10 cm of ice cover by 50–70% (Table 1). This is caused by higher absolute values for temperature gradients (T2m-Ts) for C00 (−10.9 K), leading to higher heat loss into the atmosphere and therefore higher ice production compared to the thin-ice covered polynya in C10 (−5.8 K).
As shown in Figs. 2d and 3d, ice-production rates for C10 match quite well with those calculated by Willmes et al. (2011). This seems to be surprising considering that Willmes et al. used NCEP data—which have a resolution being too coarse to resolve polynyas—for the energy flux calculation. Consequently, T2m is too low in NCEP within the polynya areas, since polynyas and their warming effects on the atmosphere are not represented adequately. Hence, using NCEP, or any other coarse-grid global analysis data that cannot resolve the polynyas, for calculating heat fluxes should lead to systematic overestimation of ice production in polynyas. While the NCEP mean T2m over polynyas is 8K colder than for C00 in 2007/08 (Fig. 2a) and 6.7 K colder in 2008/09 (Fig. 3a), the differences between NCEP and C10 amount only to 2.4 K and 1.2 K, respectively.
The differences between mean values of T2m over the polynya and the entire Laptev Sea decline from 12.6°C for C00 to 7.2°C for C10 and to 3.5°C for NCEP (Table 2). This decline originates from the decrease in sensible heat fluxes between C00 and C10 and the different consideration of polynyas in NCEP. While in NCEP, polynyas are not resolved and hence are treated as sea ice, the open water in the C00 simulations leads to a temperature about 7 K higher over polynyas compared to NCEP (Table 2). However, when comparing average temperatures of NCEP and COSMO for the whole Laptev Sea, NCEP temperatures are generally 0.9 (2.8) K higher for 2007/08 (2008/09) than COSMO temperatures. This systematic warm bias of NCEP in relation to COSMO has the same effect as the atmospheric boundary layer warming by the polynyas. This explains why the results of ice production calculation for C10 and Willmes et al. (2011) are similar.
Table 2 Seasonal (November–April) mean 2-m and surface temperatures, temperature gradients and difference (all in °C) between temperatures over the polynya (Pol) and the entire Laptev Sea (Lap) for the winters 2007/08 and 2008/09 for Consortium for Small-scale Modelling (COSMO) data for ice-free (C00) conditions and 10 cm of sea-ice cover (C10) and National Centers for Environmental Prediction reanalysis data set (NCEP). The Laptev Sea area is the sea part of the COSMO 5 km model area (Fig. 1).
| |
2-m temperature (T2m) |
Surface temperature (Ts) |
Temperature gradient (T2m-Ts) |
| |
Polynya |
Laptev Sea |
Pol-Lap |
Polynya |
Laptev Sea |
Pol-Lap |
Polynya |
Laptev Sea |
| NCEP |
−19.9 |
−23.4 |
3.5 |
−20.6 |
−24.5 |
3.9 |
0.7 |
1.1 |
| C00 |
−12.6 |
−25.2 |
12.6 |
−1.7 |
−26.3 |
24.6 |
−10.9 |
1.1 |
| C10 |
−18.1 |
−25.3 |
7.2 |
−12.3 |
−26.6 |
14.3 |
−5.8 |
1.3 |
The difference between NCEP-T2m and COSMO-T2m is even greater when looking at daily values (Figs. 2a, 3a). Mean air temperature over the polynya is only shown if the polynya size is larger than 300 km2 (corresponding to 10 model grid points). Mean T2m at polynyas from C00/C10 exceed the NCEP-T2m by 7.3/1.8°C on average and up to 20/8°C for single days. Polynya ice production would be higher when using NCEP-T2m instead of COSMO-T2m because the surface layer instability would be stronger (Table 2).
Regional ice production
Figure 4 shows ice production rates and ice production of the polynyas of the Laptev Sea sub-regions—north-eastern Taimyr (NET), Taimyr (T), Anabar–Lena (AL) and western New Siberian (WNS)—for both winters. The production rates are calculated by dividing the seasonal sum of ice production in a sub-region by the seasonal sum of polynya area in the same sub-region. Generally, largest ice production rates can be found for C00 and the smallest by Willmes et al. (2011). The NET is the most productive polynya in terms of volume ice production in both years. While largest growth rates (m d−1) occur in the WNS polynyas in 2008/09, the total contribution of this sub-region to ice production is small due to a generally smaller polynya size. Differences in ice production sums between that generated by Willmes et al. (2011) and C10 are also caused by slightly different polynya areas (Figs. 2c, 3c). Calculations of polynya area by Willmes et al. are larger for most small polynya openings, which results in modest differences for regional ice production compared to C10.
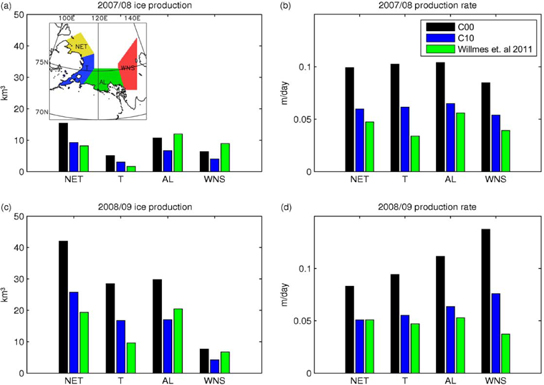
Fig. 4
(a, c) Total seasonal ice production and (b, d) mean production rates for polynyas in the Laptev Sea in the study by Willmes et al. (2011) and as generated by the model of the Consortium for Small-scale Modelling (COSMO) for ice-free (C00) conditions and 10 cm of sea-ice cover (C10). See inset in (a) for location of the sub-regions: north-eastern Taimyr (NET), Taimyr (T), Anabar–Lena (AL) and western New Siberian (WNS).
Figure 5 displays the regional distribution of the ice production in the Laptev Sea. It is generated by accumulating the ice production of one season for every pixel. The highest ice production rates occur in the western Laptev Sea, in the NET sub-region (Fig. 4), with up to 5 m per season for C00 and 3 m for C10, respectively. This kind of regional distribution differs from that of Tamura & Ohshima (2011), who show the maximum of ice production (5 m) in the area of AL. While the NET polynya is relatively broad in both years, ice production in the other sub-regions occurs in more narrow zones at the fast-ice edge. This highlights the importance of high-resolution atmospheric simulations in providing an appropriate description of air–sea interaction and ice production for Arctic flaw polynyas.
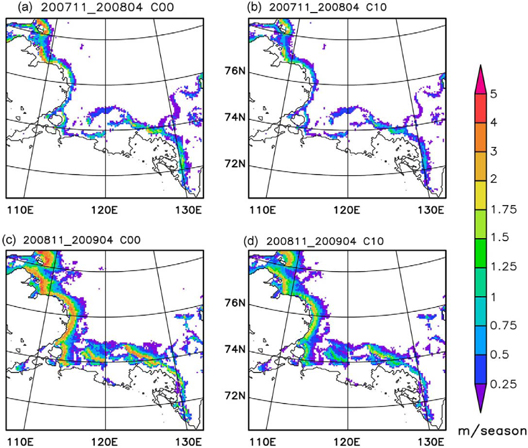
Fig. 5
Maps of the sum of ice production in (a, b) November–April 2007/08 and (c, d) November–April 2008/09; and in (a, c) ice-free polynyas (C00) and (b, d) polynyas with 10 cm of ice cover (C10).
Frequency distribution of total daily ice production
The frequency distribution of total daily ice production for both winters is shown in Fig. 6. The distribution shifts to the right from 2007/08 to 2008/09, which means that the percentage of days with high ice production is generally higher for winter 2008/09. This corresponds well with larger polynya openings in 2008/09 (Fig. 5). During about 20% of the observation period, no polynyas are observed at all for C00/C10 and consequently related polynya ice production is zero. Low ice production occurs less frequently than as shown by Willmes et al. (2011). In contrast, high production occurs more frequently for C00/10 than in simulations by Willmes et al. (2011). Differences between C10 and C00 are reflected by an increased number of days with high ice production for C00. Two main conclusions can be drawn from Fig. 6: (1) C00 leads to more extreme ice production events than C10; and (2) the variability of ice production is generally lower in simulations by Willmes et al. (2011) than for C00/C10, which is caused by differences in the methods for deducing polynya area and atmospheric data.
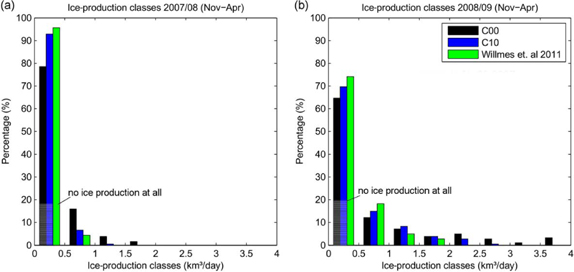
Fig. 6
Frequency distribution of total daily ice production in (a) 2007/08 and (b) 2008/09 in the study by Willmes et al. (2011) and as generated by the model of the Consortium for Small-scale Modelling (COSMO) for ice-free (C00) conditions and 10 cm of sea-ice cover (C10). Hatching indicates percentage of days without ice production.
Discussion
Wintertime ice production in the Laptev Sea and associated dense water formation have been investigated in a wide range of studies using salinity measurements (Dmitrenko et al. 2009), wind-driven polynya models (Dethleff et al. 1998; Winsor & Björk 2000) and satellite sea-ice data (Martin & Cavalieri 1989; Cavalieri & Martin 1994; Rigor & Colony 1997; Tamura & Oshima 2011; Willmes et al. 2011) to derive polynya area and associated ice production.
A comparison between our results and previous studies yields a good agreement with the satellite-based method of Willmes et al. (2011) for C10 in terms of annual ice production: 30 km3 (C10) compared to 34 km3 (Willmes et al.) in 2007/08, and 73 km3 (C10) compared to 59 km3 (Willmes et al.) in 2008/09. Regional distributions are similar during winter 2007/08, but differ for winter 2008/09, showing higher ice production for C10 in the western Laptev Sea polynyas compared to that estimated by Willmes et al. (2011). In comparison with the mean distribution for the complete 28-year time series of Willmes et al. (2011), the ice production is unusually high in the NET and T sub-region in winter 2008/09.
The study by Dethleff et al. (1998) yielded a seasonal ice production in Laptev polynyas of 258 km3 for the winter 1991/92, which is much larger than any year for the period 1979–2008 shown by Willmes et al. (2011), who calculate a value of 63 km3 for the winter 1991/92—a quarter of the ice production arrived at by Dethleff et al. (1998). These large differences cannot be explained by interannual variability since the standard deviation used by Willmes et al. (2011) for ice production for the 20-year period is negligible compared to this difference for winter 1991/92.
Tamura & Ohshima (2011) investigated ice production in Arctic polynyas for the period 1992–2007. For the Laptev Sea, this study yields a mean seasonal ice production of about 100 km3 for the months November–April, which exceeds that of Willmes et al. (2011) by a factor of two. It is also considerably higher than the largest value of the present study. Comparing the results of the present study with those of Tamura & Ohshima (2011) is difficult. In their study, ice production occurs in the AL sub-region area very close to the shoreline in a region that is covered with fast ice during winter, which is not realistic. While Willmes et al. (2011) show the WNS sub-region as a major contributor to the total ice production, this area shows negligible contributions in the study by Tamura & Ohshima (2011). Additionally, their method of parameterizing shortwave radiation with the help of empirical formulae is arguable since it implies errors in all months with incoming shortwave radiation (September/October/April/May). However, these last two points should result in less ice production compared to our study, which is not the case. As the seasonal sum of ice production is determined by multiple factors (including radiation flux computations, parameterization of turbulent heat fluxes, treatment of thin ice, atmospheric forcing), comparisons between different studies are generally difficult. Therefore the actual effect of the advantages of the present study like improved calculation of energy fluxes and a better physical basis cannot be quantified exactly. Nevertheless, our results clearly indicate that the estimations of ice production in the Laptev Sea by Tamura & Ohshima (2011) tend to be overestimated.
The assumption that atmospheric forcing from NCEP data, as used by Willmes et al. (2011), leads to notably increased T2m in comparison to COSMO-T2m could be verified for open-water polynyas (C00). Here the differences for T2m are quite large (up to 10 K; see Figs. 2, 3). For thin-ice covered polynyas a warm bias of NCEP-T2m in comparison to COSMO-T2m partly compensates expected differences. There is therefore only a small overall temperature difference between NCEP and C10. However, the comparison of NCEP and C00 shows that large differences can be expected for the ice production in open-water polynyas.
Winsor & Björk (2000) estimated the ice production in the Laptev Sea as 6–8 km3 per winter season as an average between 1958 and 1997, which is much lower than in our study. However, we also have to keep in mind that their study includes only open-water areas and does not account for surface heat loss and ice production in areas covered by thin ice.
For the whole Laptev Sea, the net sea-ice production during wintertime was estimated to amount to 1000±500 km3 by Dmitrenko et al. (2009). This value represents the entire net ice production including autumn freeze-up over the entire shelf. Putting the results of Dmitrenko et al. (2009) in relation to our findings we obtain a contribution of polynyas to the entire Laptev Sea ice production that is not higher than about 5%.
Summary and conclusions
We present a model-based, two-winter study with an improved method to estimate ice production in Laptev Sea polynyas. Surface energy fluxes for the calculation of ice production are provided by high-resolution simulations with the COSMO model including a thermodynamic sea-ice module (Schröder et al. 2011). For areas that are classified as polynyas (AMSR-E ice concentration below 70%), either open water polynya (C00) or 10 cm thin ice (C10) is assumed. Hence, the effects of polynyas on the atmosphere are included. Model verification using in-situ data close to the polynya and satellite-derived sea-ice Ts shows a good quality of the COSMO simulations. Total winter ice production for the Laptev Sea polynyas amounts to 30 km3 for C10 and 49 km3 for C00 in 2007/08 and to 73 km3 for C10 and 123 km3 for C00 in 2008/09. There is not only a big difference between the two winter periods, but also a high variability at monthly and daily time scales. In the C10 simulations monthly ice production varies from 0.4 to 27 km3 and daily ice production from 0 to 3 km3. Peak daily ice production exceeds 5 km3 for C00. These large differences between the 0 and 10 cm results demonstrate the big impact of thin ice.
As different polynya studies (e.g., Markus & Burns 1995; Dethleff et al. 1998; Winsor & Björk 2000; Tamura & Ohshima 2011) use different methods to infer the polynya area, resulting values for ice production differ notably. The method chosen to calculate atmospheric heat fluxes and to determine ice production in polynyas has a large influence on the results as well. We propose high-resolution mesoscale modelling as a tool to estimate ice production. In contrast to most satellite-based methods, the state-of-the-art computation of radiative and turbulent fluxes is inherent in modern mesoscale models, which is a precondition for calculating ice production accurately. In addition, the ability of high-resolution atmospheric forcing to resolve small-scale structures is a key factor for realistically assessing ice production in many narrow flaw polynyas. However, it is also crucial to consider thin-ice distribution within polynyas.
In conclusion, the results of the present study suggest that most previous studies have greatly overestimated ice production in the Laptev polynyas. Dethleff et al. (1998) estimate a production of 258 km3 (only 1990/91), and the satellite-based study of Tamura & Ohshima (2011) yields a value of about 100 km3 (1992–2007). Our model-based estimate is in agreement with the SSM/I-based study by Willmes et al. (2011), which yields 55±15 km3 for the period 1979–2008. A further perspective for the calculation of polynya ice production could be high-resolution coupled sea ice–ocean–atmosphere models, which can simulate thin-ice distribution that can then be verified using ice-thickness data derived from MODIS Ts (Adams et al. 2013).
Acknowledgements
The German Meteorological Service kindly provided the COSMO model and the German Meteorological Service’s global model analyses. We thank the German Climate Computing Centre, where we performed our simulations. AMSR-E data were provided by the University of Hamburg. This work was funded by the German Ministry for Education and Research Laptev Sea System project (grant no. 03G0759D).
References
Adams
S., Willmes
S., Heinemann
G., Rozman
P., Timmermann
R. & Schröder
D. 2011. Evaluation of simulated sea-ice concentrations from sea-ice/ocean models using satellite data and polynya classification methods. Polar Research
30, 7124, doi: 10.3402/polar.v30i0.7124.
Publisher Full Text
Adams
S., Willmes
S., Schröder
D., Heinemann
G., Bauer
M. & Krumpen
T. 2013.
Improvement and sensitivity analysis of thermal thin-ice thickness retrievals. IEEE Transactions on Geoscience and Remote Sensing 51,
3306–3318.
Publisher Full Text
Barber
D.G. & Massom
R.A. 2007.
The role of sea ice in Arctic and Antarctic polynyas.
In W.O. Smith & D.G. Barber (eds.): Polynyas. Windows to the world. Pp. 1–54. Amsterdam: Elsevier.
Bromwich
D.H., Cassano
J.J., Klein
T., Heinemann
G., Hines
K.M., Steffen
K. & Box
J.E. 2001.
Mesoscale modeling of katabatic winds over Greenland with Polar MM5. Monthly Weather Review 129,
2290–2309.
Bromwich
D.H., Monaghan
A.J., Manning
K.W. & Powers
J.G. 2005.
Real-time forecasting for the Antarctic: an evaluation of the Antarctic Mesoscale Prediction System (AMPS). Monthly Weather Review 133,
579–603.
Publisher Full Text
Cavalieri
D.J. & Martin
S. 1994.
The contribution of Alaskan, Siberian, and Canadian coastal polynyas to the cold halocline layer of the Arctic Ocean. Journal of Geophysical Research—Oceans 99,
18343–18362.
Publisher Full Text
Dethleff
D., Loewe
P. & Kleine
E. 1998.
Laptev Sea flaw lead: detailed investigation on ice formation and export during 1991/1992 winter season. Cold Regions Science and Technology 27,
225–243.
Publisher Full Text
Dmitrenko
I.A., Kirillov
S.A., Tremblay
L.B., Bauch
D. & Willmes
S. 2009. Sea-ice production over the Laptev Sea shelf inferred from historical summer-to-winter hydrographic observations of 1960s–1990s. Geophysical Research Letters
36, L13605, doi: 10.1029/2009GL038775.
Publisher Full Text
Doms
G., Förstner
J., Heise
E., Herzog
H.-J., Mironov
D., Raschendorfer
M., Reinhardt
T., Ritter
B., Schrodin
R., Schulz
J.-P. & Vogel
G. 2011. A description of the nonhydrostatic regional COSMO model. Part ii: physical parameterization. Offenbach am Main: German Meteorological Service.
Ebner
L., Schröder
D. & Heinemann
G. 2011. Impact of Laptev Sea flaw polynyas on the atmospheric boundary layer and ice production using idealized mesoscale simulations. Polar Research
30, 7210, doi: 10.3402/polar.v30i0.7210.
Publisher Full Text
Ernsdorf
T., Schröder
D., Adams
S., Heinemann
G., Timmermann
R. & Danilov
S. 2011. Impact of atmospheric forcing data on simulations of the Laptev Sea polynya dynamics using the sea-ice ocean model FESOM. Journal of Geophysical Research—Oceans
116, C12038, doi: 10.1029/2010JC006725.
Publisher Full Text
Gutjahr
O. & Heinemann
G. 2013. Comparing precipitation bias correction methods for high-resolution regional climate simulations using COSMO-CLM—effects on extreme values and climate change signal. Theoretical and Applied Climatology, doi: 10.1007/s00704-013-0834-z.
Heinemann
Heinemann G., Helbig A. & Ernsdorf T. 2010. Meteorological measurements at the ice edge of the West New Siberian Polynya. In H. Kassens (ed.): System Laptev-See: Eurasische Schelfmeere im Umbruch: Ozeanische Fronten und Polynjasysteme in der Laptev-See. Schlussbericht FKZ 03G0639. (Laptev Sea system: the Eurasian shelf seas in the Arctic’s changing environment: frontal zones and polynya systems in the Laptev Sea. Final report 03G0639.) Pp. I11–I12. Kiel, Germany: Secretariat of the Laptev Sea System, IFM-GEOMAR.
Helbig A., Adams S. & Heinemann G. 2010. Meteorological measurements at the ice edge of the West New Siberian Polynya. In H. Kassens (ed.): System Laptev-See: Eurasische Schelfmeere im Umbruch: Ozeanische Fronten und Polynjasysteme in der Laptev-See. Schlussbericht FKZ 03G0639. (Laptev Sea system: the Eurasian shelf seas in the Arctic’s changing environment: frontal zones and polynya systems in the Laptev Sea. Final report 03G0639.) Pp. J21–J26. Kiel, Germany: Secretariat of the Laptev Sea System, IFM-GEOMAR.
Kanamitsu
M., Ebisuzaki
W., Woollen
J., Yang
S.-K., Hnilo
J.J., Fiorino
M. & Potter
G.L. 2002.
NCEP-DOE AMIP-II Reanalysis 2 (R-2). Bulletin of the American Meteorological Society 83,
1631–1643.
Publisher Full Text
Louis
J.-F. 1979.
A parametric model of vertical eddy fluxes in the atmosphere. Boundary-Layer Meteorology 17,
187–202.
Publisher Full Text
Majewski
D., Liermann
D., Prohl
P., Ritter
B., Buchhold
M., Hanisch
T., Paul
G., Wergen
W. & Baumgardner
J. 2002.
The operational global icosahedral–hexagonal gridpoint model GME: description and high-resolution tests. Monthly Weather Review 130,
319–338.
Markus
T. & Burns
B.A. 1995.
A method to estimate subpixel-scale coastal polynyas with satellite passive microwave data. Journal of Geophysical Research—Oceans 100,
4473–4487.
Publisher Full Text
Martin
S. & Cavalieri
D.J. 1989.
Contributions of the Siberian shelf polynyas to the Arctic Ocean intermediate and deep water. Journal of Geophysical Research—Oceans 94,
12725–12738.
Publisher Full Text
Martin
S., Drucker
R., Kwok
R. & Holt
B. 2004. Estimation of the thin ice thickness and heat flux for the Chukchi Sea Alaskan coast polynya from Special Sensor Microwave/Imager data, 1990–2001. Journal of Geophysical Research—Oceans
109, C10012, doi: 10.1029/2004JC002428.
Publisher Full Text
Massom
R.A., Harris
P.T., Michel
K.J. & Potter
M.J. 1998.
The distribution and formative processes of latent-heat polynyas in East Antarctica. Annals of Glaciology 27,
420–426.
Rabenstein
L., Krumpen
T., Hendricks
S., Koeberle
C., Haas
C. & Hoelemann
J.A. 2013.
A combined approach of remote sensing and airborne electromagnetics to determine the volume of polynya sea ice in the Laptev Sea. Cryosphere 7,
947–959.
Publisher Full Text
Rigor
I. & Colony
R. 1997.
Sea-ice production and transport of pollutants in the Laptev Sea, 1979–1993. Science of the Total Environment 202,
89–110.
Publisher Full Text
Ritter
B. & Geleyn
J.-F. 1992.
A comprehensive radiation scheme for numerical weather prediction models with potential applications in climate simulations. Monthly Weather Review 120,
303–325.
Schättler
U., Doms
G. & Schraff
C. 2012. A description of the nonhydrostatic regional COSMO-model. Part vii: user’s guide. Offenbach am Main: German Meteorological Service.
Schröder
D., Heinemann
G. & Willmes
S. 2011. The impact of a thermodynamic sea-ice module in the COSMO numerical weather prediction model on simulations for the Laptev Sea, Siberian Arctic. Polar Research
30, article no. 6334, doi: 10.3402/polar.v30i0.6334.
Publisher Full Text
Smith
S.D., Muench
R.D. & Pease
C.H. 1990.
Polynyas and leads: an overview of physical processes and environment. Journal of Geophysical Research—Oceans 95,
9461–9479.
Publisher Full Text
Spreen
G., Kaleschke
L. & Heygster
G. 2008. Sea ice remote sensing using AMSR-E 89-GHz channels. Journal of Geophysical Research—Oceans
113, C02S03, doi: 10.1029/2005JC003384.
Publisher Full Text
Steppeler
J., Doms
G., Schättler
U., Bitzer
H.W., Gassmann
A., Damrath
U. & Gregoric
G. 2003.
Meso-gamma scale forecasts using the nonhydrostatic model LM. Meteorology and Atmospheric Physics 82,
75–96.
Publisher Full Text
Stringer
W.J. & Groves
J.E. 1991.
Location and areal extent of polynyas in the Bering and Chukchi seas. Arctic 44,
164–171.
Tamura
T. & Ohshima
K.I. 2011. Mapping of sea ice production in the Arctic coastal polynyas. Journal of Geophysical Research—Oceans
116, C07030, doi: 10.1029/2010JC006586.
Publisher Full Text
Willmes
S., Adams
S., Schröder
D. & Heinemann
G. 2011. Spatio-temporal variability of polynya dynamics and ice production in the Laptev Sea between the winters of 1979/80 and 2007/08. Polar Research
30, article no. 5971, doi: 10.3402/polar.v30i0.5971.
Publisher Full Text
Winsor
P. & Björk
G. 2000.
Polynya activity in the Arctic Ocean from 1958 to 1997. Journal of Geophysical Research—Oceans 105,
8789–8803.
Publisher Full Text
Yu
Y. & Lindsay
R.W. 2003. Comparison of thin ice thickness distributions derived from RADARSAT Geophysical Processor System and advanced very high resolution radiometer data sets. Journal of Geophysical Research—Oceans
108, article no. 3387, doi: 10.1029/2002JC001319.
Publisher Full Text